题目内容
已知两点A(1,0),B(b,0),若抛物线y2=4x上存在点C使△ABC为等边三角形,则b=( )
| A、5 | ||
B、5或-
| ||
| C、4 | ||
| D、4或-2 |
考点:抛物线的简单性质
专题:圆锥曲线的定义、性质与方程
分析:过点C做x轴垂线,垂足为D,根据正三角形性质可知D为A,B的中点,坐标为(
,0)求得DC的长,从而得到C点的坐标代入抛物线方程即可求得b.
| b+1 |
| 2 |
解答:
 解:过点C做x轴垂线,垂足为D,根据正三角形性质可知D为A,B的中点,坐标为(
解:过点C做x轴垂线,垂足为D,根据正三角形性质可知D为A,B的中点,坐标为(
,0),
则DC=
•
,
∴C点坐标为(
,±
•
),代入抛物线方程得,
×4=
×3,
整理得3b2-14b-5=0,求得b=5或-
,
故选:B.
 解:过点C做x轴垂线,垂足为D,根据正三角形性质可知D为A,B的中点,坐标为(
解:过点C做x轴垂线,垂足为D,根据正三角形性质可知D为A,B的中点,坐标为(| b+1 |
| 2 |
则DC=
| 3 |
| |b-1| |
| 2 |
∴C点坐标为(
| b+1 |
| 2 |
| 3 |
| |b-1| |
| 2 |
| b+1 |
| 2 |
| b2-2b+1 |
| 2 |
整理得3b2-14b-5=0,求得b=5或-
| 1 |
| 3 |
故选:B.
点评:本题主要考查了抛物线的应用.解题的关键是充分利用正三角形的性质,求出C点的坐标.

练习册系列答案
相关题目
已知集合M={x|x2-px+6=0},N={x|x2+6x-q=0},若M∩N={2},则p+q的值为( )
| A、21 | B、8 | C、7 | D、6 |
复数z=|(
-i)i|+i5(i为虚数单位),则复数z的共轭复数为( )
| 3 |
| A、2-i | B、2+i |
| C、4-i | D、4+i |
某几何体的三视图如图所示,则该几何体的体积为( )


A、
| ||
B、
| ||
| C、1 | ||
| D、2 |
多面体MN-ABCD的底面ABCD为矩形,其正视图和侧视图如图,其中正视图为等腰梯形,侧视图为等腰三角形,则该多面体的体积是( )
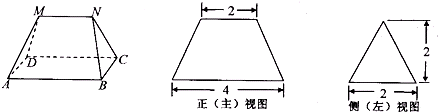

A、
| ||||
B、
| ||||
C、
| ||||
D、
|