题目内容
若函数f（x）=ax3+bx2+cx+d（a，b，c＞0）在R上是单调函数，则
的取值范围为（ ）
| f′(1) |
| b |
| A、（4，+∞） | ||
B、（2+2
| ||
| C、[4，+∞） | ||
D、[2+2
|
考点：利用导数研究函数的单调性
专题：导数的概念及应用
分析：利用导数求解，由函数f（x）=ax3+bx2+cx+d（a，b，c＞0）在R上是单调函数，可得f′（x）＞0恒成立，
找出a，b，c的关系，再利用基本不等式求最值．
找出a，b，c的关系，再利用基本不等式求最值．
解答：
解：∵函数f（x）=ax3+bx2+cx+d（a，b，c＞0）在R上是单调函数，
∴f′（x）＞0在R上恒成立，即3ax2+2bx+c＞0恒成立，即△=4b2-12ac≤0 即b2≤3ac，
∴
=
=
+
+2≥2
+2≥4．
故选C．
∴f′（x）＞0在R上恒成立，即3ax2+2bx+c＞0恒成立，即△=4b2-12ac≤0 即b2≤3ac，
∴
| f′(1) |
| b |
| 3a+2b+c |
| b |
| 3a |
| b |
| c |
| b |
|
故选C．
点评：考查利用导数即基本不等式的解决问题的能力，把问题转化为恒成立问题解决是本题的关键，应好好体会这种问题的转化思路．
练习册系列答案
相关题目
为了稳定市场，确保农民增收，某农产品3月以后的每月市场收购价格与其前三个月的市场收购价格有关，并使其与前三个月的市场收购价格之差的平方和最小，下表列出的是该产品今年前六个月的市场收购价格，则前七个月该产品的市场收购价格的方差为（ ）
| 月份 | 1 | 2 | 3 | 4 | 5 | 6 | 7 |
| 价格（元/担） | 68 | 78 | 67 | 71 | 72 | 70 |
A、
| ||
B、
| ||
| C、11 | ||
D、
|
已知方程
+
=1表示椭圆，则k的取值范围（ ）
| x2 |
| 3+k |
| y2 |
| 2+k |
| A、k＞-3 | B、-3＜k＜-2 |
| C、k＞-2 | D、k＜-3 |
若x，y满足约束条件
，则z=2x-y的最大值是（ ）
|
| A、4 | ||
B、
| ||
| C、1 | ||
| D、2 |
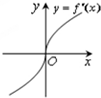已知定义在R上的函数f（x）满足f（-1）=f（3）=1，f′（x）为f（x）的导函数，且导函数y=f′（x）的图象如图所示．则不等式f（x）＜1的解集是（ ）| A、（-1，0） |
| B、（-1，3） |
| C、（0，3） |
| D、（-∞，-1）（3，+∞） |
复数
的计算结果是（ ）
| 1-2i |
| 2+i |
A、-
| ||
| B、-i | ||
| C、i | ||
D、
|
过椭圆的一个焦点F2作垂直于实轴的弦PQ，F1是另一焦点，若∠PF1Q=
，则椭圆的离心率e等于（ ）
| π |
| 2 |
A、
| ||||
B、
| ||||
C、1-
| ||||
D、1-
|