题目内容

化简：（1）
sin(540°+α)•cos(-α)
tan(α-180°)
．
（2）cosα
1-sinα
1+sinα
+sinα
1-cosα
1+cosα
（α为第四象限角）．
考点：同角三角函数基本关系的运用
专题：三角函数的求值
分析：（1）原式利用诱导公式化简，约分即可得到结果；
（2）原式利用二次根式的化简公式化简，再利用同角三角函数间基本关系变形即可得到结果．
解答： 解：（1）原式=
sin(360°+180°+α)cosα
tanα
=
-sinαcosα
tanα
=-cos2α；
（2）∵α为第四象限角，
∴sinα＜0，cosα＞0，
则原式=cosα
(1-sinα)2
|cosα|
+sinα
(1-cosα)2
|sinα|
=1-sinα-1+cosα=cosα-sinα．
点评：此题考查了同角三角函数基本关系的运用，熟练掌握基本关系是解本题的关键．
练习册系列答案
相关题目
若函数f（x）=ax3+bx2+cx+d（a，b，c＞0）在R上是单调函数，则
f′(1)
b
的取值范围为（　　）
A、（4，+∞）
B、（2+2
3
，+∞）
C、[4，+∞）
D、[2+2
3
，+∞）
已知函数f（x）=
a
2
sin2x-cos2x的图象过点（
π
8
，0）．
（Ⅰ）求实数a的值；
（Ⅱ）求函数f（x）的最小正周期及最大值．
已知函数f（x）=2sin（ωx），其中常数ω＞0．
（1）令ω=1，求函数F（x）=f（x）+f（x+
π
2
）的单调区间；
（2）令ω=2，将函数y=f（x）的图象向左平移
π
6
个单位，再往上平移1个单位，得到函数y=g（x）的图象．对任意的a∈R，求y=g（x）在区间[a，a+10π]上零点个数的所有可能值．
根据以往统计资料，某地车主购买甲种保险的概率为0.5，购买乙种保险但不购买甲种保险的概率为0.3，设各车主购买保险相互独立．
（Ⅰ）求该地1位车主至少购买甲、乙两种保险中的l种的概率；
（Ⅱ）X表示该地的3位车主中，甲、乙两种保险都不购买的车主数，求X的分布列和期望．
如表给出一个“三角形数阵”：
1
4
   
1
2
1
4
  
3
4
3
8
3
16
 
…   
已知每一列的数成等差数列，从第三行起，每一行的数成等比数列，每一行的公比都相等，记第i行第j列的数为aij（i≥j，i，j∈N*），
（1）求a83；
（2）试写出aij关于i，j的表达式；
（3）记第n行的和为An，求数列{An}的前m项和Bm的表达式．
定义运算：
.
ab
cd
.
=ad-bc．
（1）若角α是△ABC的一个内角，且
.
sinαcosα
-11
.
=
1
5
，请判断△ABC形状并求sinα-cosα的值；
（2）求f（x）=
.
cosx4
msinxcosx
.
-3m（m∈R）的最大值．
为了解某校学生的视力情况，现采用随机抽样的方式从该校的A，B两班中各抽5名学生进行视力检测．检测的数据如下：
A班的5名学生的视力检测结果：4.3，5.1，4.6，4.1，4.9．
B班的5名学生的视力检测结果：5.1，4.9，4.0，4.0，4.5．
（Ⅰ）分别计算两组数据的平均数，从计算结果看，哪个班的学生视力较好？
（Ⅱ）由数据判断哪个班的5名学生视力方差较大？（结论不要求证明）
（Ⅲ）现从A班的上述5名学生中随机选取3名学生，用X表示其中视力大于4.6的人数，求X的分布列和数学期望．
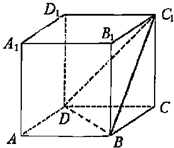已知ABCD-A1B1C1D1是棱长为1的正方体．
（1）求异面直线BC1与B1D1所成的角．
（2）求直线BC1与平面ABCD所成的角．
（3）求二面角C1-BD-A的正切值．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网