题目内容
已知:
=(2cosωx,sinωx),
=(sin(ωx+
),2
cosωx),且f(x)=
•
+t-1,若f(x)的图象上两个最高点的距离为3π,且当0<x<π时,函数f(x)的最小值为0.求表达式.
| m |
| n |
| π |
| 2 |
| 3 |
| m |
| n |
考点:平面向量数量积的运算,三角函数中的恒等变换应用
专题:三角函数的图像与性质,平面向量及应用
分析:首先利用向量的数量积运算得到f(x)的解析式,然后利用倍角公式化简三角函数式,利用三角函数性质求参数.
解答:
解:由已知f(x)=
•
+t-1=2cosωxsin(ωx+
)+sinωx2
cosωx+t-1
=2cosωxcosωx+sinωx2
cosωx+t-1
=2cos2ωx+
sin2ωx+t-1
=cos2ωx+
sin2ωx+t
=2sin(2ωx+
)+t,
因为f(x)的图象上两个最高点的距离为3π,所以f(x)的周期为3π,所以ω=
,所以f(x)=2sin(
x+
)+t,
且当0<x<π时,函数f(x)的最小值为0,所以(
x+
)∈(
,
),f(x)=2sin(
x+
)+t的最小值为
+t=0,所以t=-
,
所以f(x)=2sin(
x+
)-
.
| m |
| n |
| π |
| 2 |
| 3 |
=2cosωxcosωx+sinωx2
| 3 |
=2cos2ωx+
| 3 |
=cos2ωx+
| 3 |
=2sin(2ωx+
| π |
| 6 |
因为f(x)的图象上两个最高点的距离为3π,所以f(x)的周期为3π,所以ω=
| 1 |
| 3 |
| 2 |
| 3 |
| π |
| 6 |
且当0<x<π时,函数f(x)的最小值为0,所以(
| 2 |
| 3 |
| π |
| 6 |
| π |
| 6 |
| 5π |
| 6 |
| 2 |
| 3 |
| π |
| 6 |
| 1 |
| 2 |
| 1 |
| 2 |
所以f(x)=2sin(
| 2 |
| 3 |
| π |
| 6 |
| 1 |
| 2 |
点评:本题考查了向量数量积公式的运用以及三角函数解析式的化简,运用了倍角公式等等价变换.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
已知集合{(x,y)|
}表示的平面区域为Ω,若在区域Ω内任取一点P(x,y),则点P的坐标满足不等式x2+y2≤2的概率为( )
|
A、
| ||
B、
| ||
C、
| ||
D、
|
 阅读如图所示的程序,则输出的S是( )
阅读如图所示的程序,则输出的S是( )| A、17 | B、19 | C、21 | D、23 |
函数f(x)=
,若f(x0)≤
,则x0的取值范围是( )
|
| 3 |
| 2 |
A、(log2
| ||||
B、(0,log2
| ||||
C、[0,log2
| ||||
D、(log2
|
三个学校分别有1名、2名、3名学生获奖,这6名学生要排成一排合影,则同校学生排在一起的概率是( )
A、
| ||
B、
| ||
C、
| ||
D、
|
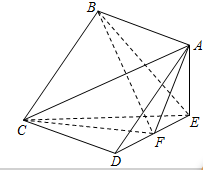 如图,在四棱锥E-ABCD中,底面ABCD为正方形,AE⊥平面CDE,已知AE=DE=2,F为线段DE的中点.
如图,在四棱锥E-ABCD中,底面ABCD为正方形,AE⊥平面CDE,已知AE=DE=2,F为线段DE的中点.