题目内容
已知函数f(x)=log2(1+x)+alog2(1-x)为奇函数,解不等式:f-1(x)<
.
| 1 |
| 2 |
考点:指、对数不等式的解法,函数奇偶性的判断,反函数
专题:计算题,函数的性质及应用,不等式的解法及应用
分析:求出定义域,再由奇函数的定义,可得f(-x)+f(x)=0,可得a=-1,再由反函数的求法,求得f-1(x)=
,再由指数函数的单调性,即可解出不等式.
| 2x-1 |
| 2x+1 |
解答:
解:由1-x>0,且1+x>0,
可得-1<x<1,
即定义域为(-1,1),
由f(x)为奇函数,
则f(-x)+f(x)=0,
即log2(1-x)+alog2(1+x)+log2(1+x)+alog2(1-x)=0,
即log2(1-x2)+alog2(1-x2)=0,
即有a=-1,
则f(x)=log2(1+x)-log2(1-x)=log2
由
=2y,解得x=
,
则有f-1(x)=
,
则f-1(x)<
即为
<
,
即1-
<
,即2x<3,
解得x<log23.
则解集为(-∞,log23).
可得-1<x<1,
即定义域为(-1,1),
由f(x)为奇函数,
则f(-x)+f(x)=0,
即log2(1-x)+alog2(1+x)+log2(1+x)+alog2(1-x)=0,
即log2(1-x2)+alog2(1-x2)=0,
即有a=-1,
则f(x)=log2(1+x)-log2(1-x)=log2
| 1+x |
| 1-x |
由
| 1+x |
| 1-x |
| 2y-1 |
| 2y+1 |
则有f-1(x)=
| 2x-1 |
| 2x+1 |
则f-1(x)<
| 1 |
| 2 |
| 2x-1 |
| 2x+1 |
| 1 |
| 2 |
即1-
| 2 |
| 2x+1 |
| 1 |
| 2 |
解得x<log23.
则解集为(-∞,log23).
点评:本题考查函数的奇偶性的运用,考查反函数的求法及指数不等式的解法,考查指数函数的性质的运用,考查运算能力,属于中档题.

练习册系列答案
相关题目
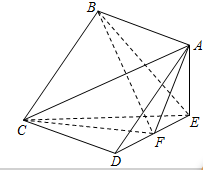 如图,在四棱锥E-ABCD中,底面ABCD为正方形,AE⊥平面CDE,已知AE=DE=2,F为线段DE的中点.
如图,在四棱锥E-ABCD中,底面ABCD为正方形,AE⊥平面CDE,已知AE=DE=2,F为线段DE的中点.