题目内容
在矩形ABCD中，AB=1，AD=
，P为矩形内一点，且AP=
．若
=λ
+μ
（λ，μ∈R），则λ+
μ的最大值为（ ）
| 3 |
| ||
| 2 |
| AP |
| AB |
| AD |
| 3 |
A、
| ||||||
B、
| ||||||
C、
| ||||||
D、
|
考点：平面向量的基本定理及其意义
专题：平面向量及应用
分析：可根据条件画出图形，根据图形设∠PAE=θ，且0≤θ≤
，则
又可用
，
表示为：
=
cosθ
+
sinθ
．所以根据平面向量基本定理得到：
，所以λ+
μ=
(cosθ+sinθ)=
sin(θ+
)，sin(θ+
)最大值为1，所以λ+
μ的最大值为
．
| π |
| 2 |
| AP |
| AB |
| AD |
| AP |
| ||
| 2 |
| AB |
| 1 |
| 2 |
| AD |
|
| 3 |
| ||
| 2 |
| ||
| 2 |
| π |
| 4 |
| π |
| 4 |
| 3 |
| ||
| 2 |
解答：
解：如图，设∠PAE=θ，0≤θ≤
，则：
=
+
=
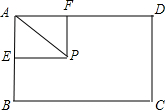
cosθ
+
=
cosθ
+
sinθ
；
又
=λ
+μ
；
∴
；
∴λ+
μ=
(cosθ+sinθ)=
sin(θ+
)≤
；
∴λ+
μ的最大值为
．
故选B．
| π |
| 2 |
| AP |
| AE |
| AF |
| ||
| 2 |
| AB |
| ||||
|
| AD |
| ||
| 2 |
| AB |
| 1 |
| 2 |
| AD |
又
| AP |
| AB |
| AD |
∴
|
∴λ+
| 3 |
| ||
| 2 |
| ||
| 2 |
| π |
| 4 |
| ||
| 2 |
∴λ+
| 3 |
| ||
| 2 |
故选B．
点评：考查共线向量基本定理，两角和的正弦公式，正弦函数sinx的最大值，以及平面向量基本定理．
练习册系列答案
相关题目
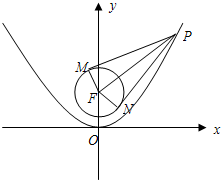已知抛物线C：x2=2py（p＞0）的焦点为F，点A（a，4）为抛物线C上的定点，点P为抛物线C上的动点．且△FOA的外接圆圆心到准线的距离为