Question

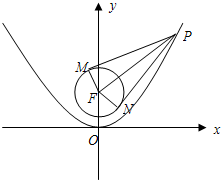已知抛物线C：x²=2py（p＞0）的焦点为F，点A（a，4）为抛物线C上的定点，点P为抛物线C上的动点．且△FOA的外接圆圆心到准线的距离为

3

2

．
（1）求抛物线C的方程；
（2）过P作圆x²+（y-1）²=

1

4

的两条切线分别交该圆于点M，N，求四边形PMFN面积的最小值及此时P点坐标．
（3）设点T（0，t），且对抛物线C上的任意动点P，∠TPF总为锐角，求实数t的取值范围．

Answer 1

考点：直线与圆锥曲线的综合问题,抛物线的标准方程

专题：综合题,圆锥曲线的定义、性质与方程

分析：（1）由题意得出圆心的纵坐标为

p

4

，由圆心到准线的距离等于

3

2

，求出p的值，则抛物线方程可求；
（2）S_PMFN=2S_△PMF=2

1

2

|PM||MF|=

1

2

|PM|，即可求四边形PMFN面积的最小值及此时P点坐标．
（3）根据题意：∠TPF为锐角⇒

PT

•

PF

＞0且t≠

p

2

，利用向量的数量积公式，可得

PT

•

PF

=y₀²-（t-3）y₀+t，记：f（y₀）=y₀²-（t-3）y₀+t在y₀∈[0，+∞）上恒成立，分类讨论，即可求实数t的取值范围．

解答： 解：（1）△FOA的外接圆的圆心在线段OF的中垂线y=

p

4

上，则圆心的纵坐标为

p

4

故到准线的距离为

p

2

+

p

4

=

3

2

从而p=2…（2分）
即抛物线C的方程为：x²=4y．…（4分）
（2）设P（x₀，y₀），则
∵圆心坐标（0，1）是抛物线C的焦点F
∴|PF|=y₀+1…（6分）
SPMFN=2S△PMF=2•

1

2

•|PM|•|MF|=

1

2

|PM|=

1

2

|PF|2- 1 4

=

1

2

(y0+1)2- 1 4

  (y0≥0)…（8分）
∴当y₀=0时，四边形PMFN面积的最小值为

3

4

，此时点P（0，0）．…（10分）
（3）（理）根据题意：∠TPF为锐角⇒

PT

•

PF

＞0且t≠

p

2

∵

PT

=（-x₀，t-y₀），

PF

=（-x₀，1-y₀），
∴

PT

•

PF

=y₀²-（t-3）y₀+t…（11分）
记：f（y₀）=y₀²-（t-3）y₀+t在y₀∈[0，+∞）上恒成立
又f（y₀）=（y₀-

t-3

2

）²-

t2-10t+9

4

．
当

t-3

2

≥0时，即：t∈[3，+∞）
当y₀=

t-3

2

时，f（y₀）_min=-

t2-10t+9

4

＞0解得：1＜t＜9，
∴t∈[3，9]；
当

t-3

2

＜0时，即：t∈（-∞，3）当y₀=0时，f（y₀）_min=t＞0，
∴t∈（0，3）…（15分）
综合得：t∈（0，1）∪（1，9）（16分）

点评：本题考查了抛物线的标准方程，考查了直线与圆锥曲线的关系，考查了方程思想和函数思想，考查学生分析解决问题的能力，属于中档题．