题目内容
已知函数f(x)=
+
(-1<x<1,且x≠0).
(Ⅰ)求f(x)的最小值;
(Ⅱ)若|t+1|≤f(x)恒成立,求实数t的取值范围.
| 1 |
| x2 |
| 4 |
| 1-x2 |
(Ⅰ)求f(x)的最小值;
(Ⅱ)若|t+1|≤f(x)恒成立,求实数t的取值范围.
考点:柯西不等式
专题:计算题,不等式的解法及应用
分析:(Ⅰ)由柯西不等式f(x)=
+
=[x2+(1-x2)](
+
)≥[x•
+
•
]2=9,即可得到最小值;
(Ⅱ)由(Ⅰ)知,|t+1|≤f(x)恒成立即为|t+1|不大于f(x)的最小值为9,解得即可得到t的取值范围.
| 1 |
| x2 |
| 4 |
| 1-x2 |
| 1 |
| x2 |
| 4 |
| 1-x2 |
| 1 |
| x |
| 1-x2 |
| 2 | ||
|
(Ⅱ)由(Ⅰ)知,|t+1|≤f(x)恒成立即为|t+1|不大于f(x)的最小值为9,解得即可得到t的取值范围.
解答:
解:(Ⅰ)因为-1<x<1,且x≠0,所以1-x2>0,
由柯西不等式f(x)=
+
=[x2+(1-x2)](
+
)
≥[x•
+
•
]2=9,
当且仅当
=
,即x=±
时取等号,
∴f(x)的最小值为9.
(Ⅱ)由(Ⅰ)知f(x)的最小值为9,
由题意可得|t+1|≤9,则-10≤t≤8,
则实数t的取值范围为[-10,8].
由柯西不等式f(x)=
| 1 |
| x2 |
| 4 |
| 1-x2 |
| 1 |
| x2 |
| 4 |
| 1-x2 |
≥[x•
| 1 |
| x |
| 1-x2 |
| 2 | ||
|
当且仅当
| x | ||
|
| ||||
|
| ||
| 3 |
∴f(x)的最小值为9.
(Ⅱ)由(Ⅰ)知f(x)的最小值为9,
由题意可得|t+1|≤9,则-10≤t≤8,
则实数t的取值范围为[-10,8].
点评:本题考查柯西不等式的运用:求最值,考查不等式的恒成立问题转化为求函数的最值,考查运算能力,属于中档题和易错题.

练习册系列答案
 同步练习西南大学出版社系列答案
同步练习西南大学出版社系列答案 补充习题江苏系列答案
补充习题江苏系列答案 学练快车道口算心算速算天天练系列答案
学练快车道口算心算速算天天练系列答案
相关题目
在矩形ABCD中,AB=1,AD=
,P为矩形内一点,且AP=
.若
=λ
+μ
(λ,μ∈R),则λ+
μ的最大值为( )
| 3 |
| ||
| 2 |
| AP |
| AB |
| AD |
| 3 |
A、
| ||||||
B、
| ||||||
C、
| ||||||
D、
|
与函数y=x有相同图象的一个函数是( )
A、y=
| ||
B、y=(
| ||
| C、y=logaax(a>o,a≠1) | ||
D、y=
|
以y=±x为渐近线且经过点(2,0)的双曲线方程为( )
A、
| ||||
B、
| ||||
C、
| ||||
D、
|
已知实数a,b,c满足a+b+c=1,a2+b2+c2=1,则a+b的取值范围是( )
| A、[-1,1] | ||
B、[-
| ||
C、[0,
| ||
| D、[0,2] |
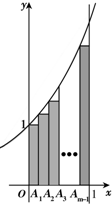 如图,A1,A2,…,Am-1(m≥2)为区间[0,1]上的m等分点,直线x=0,x=1,y=0和曲线y=ex所围成的区域为Ω1,图中m个矩形构成的阴影区域为Ω2,在Ω1中任取一点,则该点取自Ω2的概率等于
如图,A1,A2,…,Am-1(m≥2)为区间[0,1]上的m等分点,直线x=0,x=1,y=0和曲线y=ex所围成的区域为Ω1,图中m个矩形构成的阴影区域为Ω2,在Ω1中任取一点,则该点取自Ω2的概率等于