题目内容
求和:1×2+3×22+…+(2k-1)×2k.
考点:数列的求和
专题:等差数列与等比数列
分析:利用“错位相减法”和等比数列的前n项和公式即可得出.
解答:
解:设Sk=1×2+3×22+…+(2k-1)×2k,
则2Sk=22+3×23+…+(2k-3)×2k+(2k-1)×2k+1,
两式相减可得:-Sk=2+2×22+…+2×2k-(2k-1)•2k+1
=2×
-(2k-1)•2k+1-2
=2k+2-6-(2k-1)•2k+1
=(3-2k)•2k+1-6
∴Sk=(2k-3)•2k+1+6.
则2Sk=22+3×23+…+(2k-3)×2k+(2k-1)×2k+1,
两式相减可得:-Sk=2+2×22+…+2×2k-(2k-1)•2k+1
=2×
| 2(2k-1) |
| 2-1 |
=2k+2-6-(2k-1)•2k+1
=(3-2k)•2k+1-6
∴Sk=(2k-3)•2k+1+6.
点评:本题考查了“错位相减法”和等比数列的前n项和公式,考查了计算能力,属于中档题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
在矩形ABCD中,AB=1,AD=
,P为矩形内一点,且AP=
.若
=λ
+μ
(λ,μ∈R),则λ+
μ的最大值为( )
| 3 |
| ||
| 2 |
| AP |
| AB |
| AD |
| 3 |
A、
| ||||||
B、
| ||||||
C、
| ||||||
D、
|
 如图所示,已知A1B1C1-ABC是三棱柱,E、E1分别是AC、A1C1的中点.求证:平面AB1E1∥平面BEC1.
如图所示,已知A1B1C1-ABC是三棱柱,E、E1分别是AC、A1C1的中点.求证:平面AB1E1∥平面BEC1.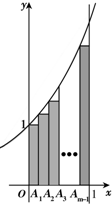 如图,A1,A2,…,Am-1(m≥2)为区间[0,1]上的m等分点,直线x=0,x=1,y=0和曲线y=ex所围成的区域为Ω1,图中m个矩形构成的阴影区域为Ω2,在Ω1中任取一点,则该点取自Ω2的概率等于
如图,A1,A2,…,Am-1(m≥2)为区间[0,1]上的m等分点,直线x=0,x=1,y=0和曲线y=ex所围成的区域为Ω1,图中m个矩形构成的阴影区域为Ω2,在Ω1中任取一点,则该点取自Ω2的概率等于