题目内容
已知A={x|-1≤x<6},B={x|m-1≤x≤3m+2},若B⊆A,求m的取值范围.
考点:集合的包含关系判断及应用
专题:集合
分析:首先,针对集合B是否为空集进行讨论,分为两种情形B=∅,B≠∅,然后,结合条件B⊆A进行求解m的取值范围.
解答:
解:①当B=∅时,即m-1>3m+2,
∴m<-
,
②当B≠∅时,
∵B⊆A,
∴
,
∴0≤m<
,
∴m的取值范围(-∞,-
)∪[0,
).
∴m<-
| 3 |
| 2 |
②当B≠∅时,
∵B⊆A,
∴
|
∴0≤m<
| 4 |
| 3 |
∴m的取值范围(-∞,-
| 3 |
| 2 |
| 4 |
| 3 |
点评:本题重点考查集合的基本运算,集合间的基本关系,数形结合思想的灵活运用等知识点,属于基础题.

练习册系列答案
 智趣寒假作业云南科技出版社系列答案
智趣寒假作业云南科技出版社系列答案
相关题目
将函数f(x)=2sin(2x-
)的图象向左平移
个单位后,所得图象的一个对称中心是( )
| π |
| 3 |
| π |
| 6 |
A、(
| ||
B、(
| ||
C、(
| ||
D、(
|
设平面向量
,
,
均为非零向量,则“
•(
-
)=0”是“
=
”的( )
| a |
| b |
| c |
| a |
| b |
| c |
| b |
| c |
| A、充分而不必要条件 |
| B、必要而不充分条件 |
| C、充分必要条件 |
| D、既不充分也不必要条件 |
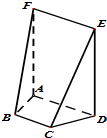 如图,在五面体ABCDEF中,四边形ADEF是正方形,FA⊥面ABCD,BC∥AD,CD=1,AD=
如图,在五面体ABCDEF中,四边形ADEF是正方形,FA⊥面ABCD,BC∥AD,CD=1,AD=