题目内容
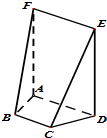 如图,在五面体ABCDEF中,四边形ADEF是正方形,FA⊥面ABCD,BC∥AD,CD=1,AD=2
如图,在五面体ABCDEF中,四边形ADEF是正方形,FA⊥面ABCD,BC∥AD,CD=1,AD=2| 2 |
(1)求证:CD⊥面ABF;
(2)试在棱DE上找一点P使得二面角B-AP-D的正切值为
| 5 |
考点:与二面角有关的立体几何综合题,直线与平面垂直的判定,二面角的平面角及求法
专题:空间位置关系与距离,空间角
分析:(1)过点B作BG∥CD,交AD于点G,可证CD⊥AB,CD⊥FA,利用线面垂直的判定定理,可得CD⊥平面ABF;
(2)过点B作BH⊥AD,垂足为H过点H作HO⊥AP,垂足为O,连结BO,可证得∠BOH即为二面角B-AP-D的平面角,设PD=t,由二面角B-AP-D的正切值为
,构造关于t的方程,解方程可得答案.
(2)过点B作BH⊥AD,垂足为H过点H作HO⊥AP,垂足为O,连结BO,可证得∠BOH即为二面角B-AP-D的平面角,设PD=t,由二面角B-AP-D的正切值为
| 5 |
解答:
证明:(1)过点B作BG∥CD,交AD于点G,则∠BGA=∠CDA=45°,
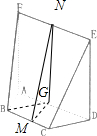
由∠BAD=45°,可得BG⊥AB,从而CD⊥AB,
又FA⊥平面ABCD,
∴CD⊥FA,
∵FA∩AB=A,
∴CD⊥平面ABF.…(6分)
(2)过点B作BH⊥AD,垂足为H过点H作HO⊥AP,垂足为O,连结BO
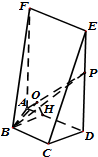
∵FA⊥面ABCD,FA?平面FADE,
∴平面FADE⊥面ABCD,
又∵BH⊥AD,平面FADE∩面ABCD=AD,BH?面ABCD=AD,
∴BH⊥平面FADE,
又∵AP?平面FADE,
∴BH⊥AP,
又∵HO⊥AP,BH∩HO=H,BH,HO?平面OBH,
∴AP⊥平面OBH,
又∵OB?平面OBH,
∴AP⊥OB,
∴∠BOH即为二面角B-AP-D的平面角,…(10分)
求得BH=AH=
,即点H为AD的四等分点
设PD=t(0<t<2
),易求得OH=
∴tan∠BOH=
=
=
解得t=
,
即当点P为DE的中点时,二面角B-AP-D的正切值为
…(14分)

由∠BAD=45°,可得BG⊥AB,从而CD⊥AB,
又FA⊥平面ABCD,
∴CD⊥FA,
∵FA∩AB=A,
∴CD⊥平面ABF.…(6分)
(2)过点B作BH⊥AD,垂足为H过点H作HO⊥AP,垂足为O,连结BO

∵FA⊥面ABCD,FA?平面FADE,
∴平面FADE⊥面ABCD,
又∵BH⊥AD,平面FADE∩面ABCD=AD,BH?面ABCD=AD,
∴BH⊥平面FADE,
又∵AP?平面FADE,
∴BH⊥AP,
又∵HO⊥AP,BH∩HO=H,BH,HO?平面OBH,
∴AP⊥平面OBH,
又∵OB?平面OBH,
∴AP⊥OB,
∴∠BOH即为二面角B-AP-D的平面角,…(10分)
求得BH=AH=
| ||
| 2 |
设PD=t(0<t<2
| 2 |
| ||
2
|
∴tan∠BOH=
| BH |
| GH |
|
| 5 |
解得t=
| 2 |
即当点P为DE的中点时,二面角B-AP-D的正切值为
| 5 |
点评:本题考查线面垂直,考查面面角,考查学生分析解决问题的能力,考查学生的计算能力,属于中档题.

练习册系列答案
相关题目
设l,m是两条不同直线,α,β是两个不同平面,则下列命题中正确的是( )
| A、若l∥α,α∩β=m,则l∥m |
| B、若l⊥α,l∥β,则α⊥β |
| C、若l∥α,m∥α,则l∥m |
| D、若l∥α,m⊥l,则m⊥α |
已知(1+i)(1-mi)=2i(i是虚数单位),则实数m的值为( )
| A、±1 | B、1 | C、2 | D、-1 |