题目内容
7.函数f(x)=4sinωx•cos(ωx+$\frac{π}{6}$)+1(ω>0),其图象上有两点A(s,t),B(s+2π,t),其中-2<t<2,线段AB与函数图象有五个交点.(Ⅰ)求ω的值;
(Ⅱ)若函数f(x)在[x1,x2]和[x3,x4]上单调递增,在[x2,x3]上单调递减,且满足等式x4-x3=x2-x1=$\frac{2}{3}$(x3-x2),求x1、x4所有可能取值.
分析 (Ⅰ)利用三角函数的诱导公式化简即可得答案;
(Ⅱ)求出函数f(x)的最值即可得答案.
解答 解:(Ⅰ)f(x)=4sinωx•cos(ωx+$\frac{π}{6}$)+1=$4sinωx•(\frac{\sqrt{3}}{2}cosωx-\frac{1}{2}sinωx)+1$
=$2\sqrt{3}sinωxcosωx+(1-2si{n}^{2}ωx)$=$\sqrt{3}sin2ωx+cos2ωx$=$2sin(2ωx+\frac{π}{6})$,
由于|AB|=2π,且线段AB与函数f(x)图象有五个交点,
因此$2T=2×\frac{2π}{2ω}=2π$,故ω=1;
(Ⅱ)由(Ⅰ)得,函数f(x)=$2sin(2ωx+\frac{π}{6})$,由题意知${x}_{3}-{x}_{2}=\frac{T}{2}=\frac{π}{2}$,
因此x4-x3=x2-x1=$\frac{2}{3}$(x3-x2)=$\frac{π}{3}$.即${x}_{1}={x}_{2}-\frac{π}{3}$,${x}_{4}={x}_{3}+\frac{π}{3}$.
∵函数f(x)在[x1,x2]上单调递增,在[x2,x3]上单调递减,
∴f(x)在x2处取得最大值,即$f({x}_{2})=2sin(2{x}_{2}+\frac{π}{6})$=2.
$2{x}_{2}+\frac{π}{6}=\frac{π}{2}+2kπ$,即${x}_{2}=\frac{π}{6}+kπ$.
∴${x}_{1}={x}_{2}-\frac{π}{3}$=$\frac{π}{6}+kπ-\frac{π}{3}=-\frac{π}{6}+kπ(k∈Z)$.
${x}_{4}={x}_{3}+\frac{π}{3}$=${x}_{2}+\frac{π}{2}+\frac{π}{3}=kπ+π(k∈Z)$.
点评 本题考查了正弦函数的图象,考查了三角函数的最值以及函数的单调性,是中档题.

 红果子三级测试卷系列答案
红果子三级测试卷系列答案 课堂练加测系列答案
课堂练加测系列答案| A. | 充分不必要条件 | B. | 必要不充分条件 | ||
| C. | 充要条件 | D. | 既不充分也不必要条件 |
| A. | (0,1) | B. | (1,2) | C. | (2,3) | D. | (3,4) |
| A. | 4 | B. | -4 | C. | ±4 | D. | 与A有关 |
| A. | f(x)是奇函数,则在(0,+∞)上是增函数 | |
| B. | f(x)是偶函数,则在(0,+∞)上是减函数 | |
| C. | f(x)既不是奇函数也不是偶函数,且在(0,+∞)上是增函数 | |
| D. | f(x)既不是奇函数也不是偶函数,且在(0,+∞)上是减函数 |
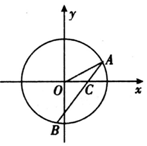 如图所示,已知A,B是单位圆上两点且|AB|=$\sqrt{3}$,设AB与x轴正半轴交于点C,α=∠AOC,β=∠OCB,则sinαsinβ+cosαcosβ=$\frac{\sqrt{3}}{2}$.
如图所示,已知A,B是单位圆上两点且|AB|=$\sqrt{3}$,设AB与x轴正半轴交于点C,α=∠AOC,β=∠OCB,则sinαsinβ+cosαcosβ=$\frac{\sqrt{3}}{2}$.