题目内容
18.“-2<m<-$\frac{1}{3}$”是“方程$\frac{{x}^{2}}{m+3}$+$\frac{{y}^{2}}{2m+1}$表示双曲线,且方程$\frac{{x}^{2}}{m+2}$-$\frac{{y}^{2}}{2m-1}$表示交点在y轴上的椭圆”的( )| A. | 充分不必要条件 | B. | 必要不充分条件 | ||
| C. | 充要条件 | D. | 既不充分也不必要条件 |
分析 根据双曲线和椭圆方程的特点求出m的取值范围,结合充分条件和必要条件的定义进行判断即可.
解答 解:若方程$\frac{{x}^{2}}{m+3}$+$\frac{{y}^{2}}{2m+1}$表示双曲线,且方程$\frac{{x}^{2}}{m+2}$-$\frac{{y}^{2}}{2m-1}$表示交点在y轴上的椭圆,
则满足$\left\{\begin{array}{l}{(m+3)(2m+1)<0}\\{-(2m-1)>m+2}\\{m+2>0}\end{array}\right.$,即$\left\{\begin{array}{l}{-3<m<-\frac{1}{2}}\\{m<-\frac{1}{3}}\\{m>-2}\end{array}\right.$,
得-2<m<-$\frac{1}{2}$,
则-2<m<-$\frac{1}{3}$是-2<m<-$\frac{1}{2}$的必要不充分条件,
即“-2<m<-$\frac{1}{3}$”是“方程$\frac{{x}^{2}}{m+3}$+$\frac{{y}^{2}}{2m+1}$表示双曲线,且方程$\frac{{x}^{2}}{m+2}$-$\frac{{y}^{2}}{2m-1}$表示交点在y轴上的椭圆”的必要不充分条件,
故选:B
点评 本题主要考查充分条件和必要条件的判断,根据双曲线和椭圆方程的定义求出m的取值范围是解决本题的关键.

练习册系列答案
 应用题作业本系列答案
应用题作业本系列答案
相关题目
8.$y=3sin(\frac{x}{2}-\frac{π}{3})$的一条对称轴是( )
| A. | $x=\frac{2π}{3}$ | B. | $x=\frac{π}{2}$ | C. | $x=-\frac{π}{3}$ | D. | $x=\frac{8π}{3}$ |
6.已知m>0,n>0,空间向量$\overrightarrow{a}$=(m,4,-3)与$\overrightarrow{b}$=(1,n,2)垂直,则mn的最大值为( )
| A. | $\frac{3}{2}$ | B. | 3 | C. | 9、 | D. | $\frac{9}{4}$ |
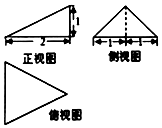 已知某三棱锥的三视图如图所示,则该三棱锥的体积为$\frac{2}{3}$,它的表面积为$2+2\sqrt{5}$.
已知某三棱锥的三视图如图所示,则该三棱锥的体积为$\frac{2}{3}$,它的表面积为$2+2\sqrt{5}$.