题目内容
17.在平面直角坐标系xOy中,向量$\overrightarrow{a}$=(x,y)所对应点位于第一象限,且在向量$\overrightarrow{b}$=(1,1)方向上的投影为$\frac{\sqrt{2}}{2}$,则$\frac{1}{x}$+$\frac{2}{y}$的最小值为3+2$\sqrt{2}$.分析 由题意可得:$\frac{\overrightarrow{a}•\overrightarrow{b}}{|\overrightarrow{b}|}$=$\frac{x+y}{\sqrt{2}}$=$\frac{\sqrt{2}}{2}$,化为x+y=1,x,y>0.再利用“乘1法”与基本不等式的性质即可得出.
解答 解:∵向量$\overrightarrow{a}$=(x,y)所对应点位于第一象限,且在向量$\overrightarrow{b}$=(1,1)方向上的投影为$\frac{\sqrt{2}}{2}$,
∴$\frac{\overrightarrow{a}•\overrightarrow{b}}{|\overrightarrow{b}|}$=$\frac{x+y}{\sqrt{2}}$=$\frac{\sqrt{2}}{2}$,化为x+y=1,x,y>0.
则$\frac{1}{x}$+$\frac{2}{y}$=(x+y)$(\frac{1}{x}+\frac{2}{y})$=3+$\frac{y}{x}+\frac{2x}{y}$≥3+2$\sqrt{\frac{y}{x}•\frac{2x}{y}}$=3+2$\sqrt{2}$,当且仅当y=$\sqrt{2}$x=2-$\sqrt{2}$.
故答案为:3+2$\sqrt{2}$.
点评 本题考查了“乘1法”与基本不等式的性质、向量投影,考查了推理能力与计算能力,属于中档题.

练习册系列答案
相关题目
8.$y=3sin(\frac{x}{2}-\frac{π}{3})$的一条对称轴是( )
| A. | $x=\frac{2π}{3}$ | B. | $x=\frac{π}{2}$ | C. | $x=-\frac{π}{3}$ | D. | $x=\frac{8π}{3}$ |
2.一直线l与平行四边形ABCD中的两边AB、AD分别交于E、F,且交其对角线AC于K,若$\overrightarrow{AB}$=2$\overrightarrow{AE}$,$\overrightarrow{AD}$=3$\overrightarrow{AF}$,$\overrightarrow{AC}$=λ$\overrightarrow{AK}$(λ∈R),则λ=( )
| A. | 2 | B. | $\frac{5}{2}$ | C. | 3 | D. | 5 |
6.已知m>0,n>0,空间向量$\overrightarrow{a}$=(m,4,-3)与$\overrightarrow{b}$=(1,n,2)垂直,则mn的最大值为( )
| A. | $\frac{3}{2}$ | B. | 3 | C. | 9、 | D. | $\frac{9}{4}$ |
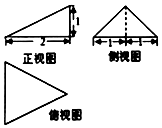 已知某三棱锥的三视图如图所示,则该三棱锥的体积为$\frac{2}{3}$,它的表面积为$2+2\sqrt{5}$.
已知某三棱锥的三视图如图所示,则该三棱锥的体积为$\frac{2}{3}$,它的表面积为$2+2\sqrt{5}$.