题目内容
3.已知双曲线C:$\frac{{x}^{2}}{{a}^{2}}-\frac{{y}^{2}}{{b}^{2}}$=1(a>0,b>0)的左、右焦点分别为F1(-c,0),F2(c,0),P是双曲线C右支上一点,且|PF2|=|F1F2|.若直线PF1与圆x2+y2=a2相切,则双曲线的离心率为( )| A. | $\frac{4}{3}$ | B. | $\frac{5}{3}$ | C. | 2 | D. | 3 |
分析 先设PF1与圆相切于点M,利用|PF2|=|F1F2|,及直线PF1与圆x2+y2=a2相切,可得几何量之间的关系,从而可求双曲线的离心率的值.
解答 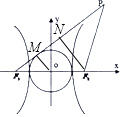 解:解:设PF1与圆相切于点M,
解:解:设PF1与圆相切于点M,
因为|PF2|=|F1F2|,所以△PF1F2为等腰三角形,N为PF1的中点,
所以|F1M|=$\frac{1}{4}$|PF1|,
又因为在直角△F1MO中,|F1M|2=|F1O|2-a2=c2-a2,所以|F1M|=b=$\frac{1}{4}$|PF1|①
又|PF1|=|PF2|+2a=2c+2a ②,
c2=a2+b2 ③
由①②③可得c2-a2=($\frac{c+a}{2}$)2,
即为4(c-a)=c+a,即3c=5a,
解得e=$\frac{c}{a}$=$\frac{5}{3}$.
故选:B.
点评 本题考查直线与圆相切,考查双曲线的定义,考查双曲线的几何性质,注意运用平面几何的性质,考查运算能力,属于中档题.

练习册系列答案
 小学课时作业全通练案系列答案
小学课时作业全通练案系列答案
相关题目
16.设首项为1,公比为$\frac{1}{3}$的等比数列{an}的前n项和Sn,则Sn=( )
| A. | $\frac{3-2{a}_{n}}{2}$ | B. | $\frac{2{a}_{n}-3}{2}$ | C. | $\frac{3-{a}_{n}}{2}$ | D. | $\frac{{a}_{n}-3}{2}$ |
14.若函数f(x)=sin2x+4cosx+ax在R上单调递减,则实数a的取值范围是( )
| A. | (-∞,-3] | B. | (-∞,-3) | C. | (-∞,6] | D. | (-∞,6) |
18.已知双曲线C:mx2+ny2=1(mn<0)的一条渐近线与圆x2+y2-6x-2y+9=0相切,则C的离心率等于( )
| A. | $\frac{5}{3}$ | B. | $\frac{5}{4}$ | C. | $\frac{5}{3}$或$\frac{25}{16}$ | D. | $\frac{5}{3}$或$\frac{5}{4}$ |
12.已知全集U={x|x≥-3},集合A={y|y=x2+4x+5},$B=\{x|y=\sqrt{1-{{log}_2}x}\}$,则(∁UA)∩B=( )
| A. | [-3,2] | B. | [-3,1) | C. | (0,1) | D. | (0,2] |
13.若焦点在y轴上的椭圆$\frac{{x}^{2}}{m}$+$\frac{{y}^{2}}{2}$=1的离心率为$\frac{2}{3}$,则m的值为( )
| A. | $\frac{8}{3}$ | B. | $\frac{2}{3}$ | C. | $\frac{10}{9}$ | D. | 以上答案均不对 |
 已知A(-3,0),B(3,0),动点P满足$\overrightarrow{PA}$•$\overrightarrow{PB}$=0,如图所示作PD⊥x轴,且$\overrightarrow{DM}$=λ$\overrightarrow{DP}$(0<λ<1)
已知A(-3,0),B(3,0),动点P满足$\overrightarrow{PA}$•$\overrightarrow{PB}$=0,如图所示作PD⊥x轴,且$\overrightarrow{DM}$=λ$\overrightarrow{DP}$(0<λ<1)