题目内容
13．若焦点在y轴上的椭圆$\frac{{x}^{2}}{m}$+$\frac{{y}^{2}}{2}$=1的离心率为$\frac{2}{3}$，则m的值为（ ）| A． | $\frac{8}{3}$ | B． | $\frac{2}{3}$ | C． | $\frac{10}{9}$ | D． | 以上答案均不对 |
分析 根据题意，由椭圆的标准方程分析可得a2=2，b2=m，由椭圆的几何性质计算可得c的值，进而由离心率公式可得有e=$\frac{c}{a}$=$\frac{\sqrt{2-m}}{\sqrt{2}}$=$\frac{2}{3}$，计算可得m的值，即可得答案．
解答 解：由题意，椭圆的方程为$\frac{{x}^{2}}{m}$+$\frac{{y}^{2}}{2}$=1，其焦点在y轴上，
其中a2=2，b2=m，则c2=2-m，
又由其离心率为$\frac{2}{3}$，则有e=$\frac{c}{a}$=$\frac{\sqrt{2-m}}{\sqrt{2}}$=$\frac{2}{3}$，
解可得m=$\frac{10}{9}$；
故选：C．
点评 本题考查椭圆的几何性质，注意椭圆的焦点在y轴上．
练习册系列答案
口算题天天练系列答案
相关题目
3．已知双曲线C：$\frac{{x}^{2}}{{a}^{2}}-\frac{{y}^{2}}{{b}^{2}}$=1（a＞0，b＞0）的左、右焦点分别为F1（-c，0），F2（c，0），P是双曲线C右支上一点，且|PF2|=|F1F2|．若直线PF1与圆x2+y2=a2相切，则双曲线的离心率为（ ）
| A． | $\frac{4}{3}$ | B． | $\frac{5}{3}$ | C． | 2 | D． | 3 |
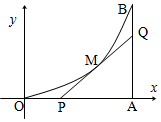如图，由y=0，x=8，y=x2围成的曲边三角形，在曲线OB弧上求一点M，使得过M所作的y=x2的切线PQ与OA，AB围城的三角形PQA的面积最大，并求得最大值．
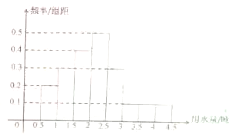某城市100户居民的月平均用水量（单位：吨），按[0.5，1），[1，1.5），[1.5，2），[2，2.5），[2.5，3），[3，3.5），[3.5，4），[4，4.5）分组的频率分布直方图如图．