题目内容
15. 已知A(-3,0),B(3,0),动点P满足$\overrightarrow{PA}$•$\overrightarrow{PB}$=0,如图所示作PD⊥x轴,且$\overrightarrow{DM}$=λ$\overrightarrow{DP}$(0<λ<1)
已知A(-3,0),B(3,0),动点P满足$\overrightarrow{PA}$•$\overrightarrow{PB}$=0,如图所示作PD⊥x轴,且$\overrightarrow{DM}$=λ$\overrightarrow{DP}$(0<λ<1)(1)求点M的轨迹方程C;
(2)过方程C对应曲线的右焦点作斜率为1的直线lAB与曲线C交于E,F两点,曲线C上是否存在点H使得△EFH的重心为坐标原点?若存在,求出λ;若不存在,请说明理由.
分析 (1)设P(x,y),则$\overrightarrow{PA}=(-3-x,-y),\overrightarrow{PB}=(3-x,-y)$,动点P满足$\overrightarrow{PA}$•$\overrightarrow{PB}$=0⇒(-3-x)(3-x)+(-y)(-y)=0化简即可.
(2)由(1)得曲线C的右焦点为(3$\sqrt{1-{λ}^{2}}$,0),斜率为1的直线lAB与的方程为:y=x-3$\sqrt{1-{λ}^{2}}$
设E(x1,y1),F(x2,y2),H(x0,y0),
假设在曲线C上存在点H使得△EFH的重心为坐标原点,则x0=-(x1+x2),y0=-(y1+y2),
联立$\left\{\begin{array}{l}{y=x-3\sqrt{1-{λ}^{2}}}\\{{λ}^{2}{x}^{2}+{y}^{2}=9{λ}^{2}}\end{array}\right.$得(${(λ}^{2}+1){x}^{2}-6\sqrt{1-{λ}^{2}}x+9-18{λ}^{2}=0$;
H($\frac{6\sqrt{1-{λ}^{2}}}{1+{λ}^{2}},\frac{-6{λ}^{2}\sqrt{1-{λ}^{2}}}{1+{λ}^{2}}$)在曲线C上,${λ}^{2}\frac{36(1-{λ}^{2})}{(1+{λ}^{2})^{2}}+\frac{36{λ}^{4}(1-{λ}^{2})}{(1+{λ}^{2})^{2}}=9{λ}^{2}$,即可求出λ.
解答 解:(1)设P(x,y),则$\overrightarrow{PA}=(-3-x,-y),\overrightarrow{PB}=(3-x,-y)$,
动点P满足$\overrightarrow{PA}$•$\overrightarrow{PB}$=0⇒(-3-x)(3-x)+(-y)(-y)=0⇒y2+x2=9
设M(s,t),∵PD⊥x轴,且$\overrightarrow{DM}$=λ$\overrightarrow{DP}$(0<λ<1),
∴x=s,y=$\frac{t}{λ}$,∴${s}^{2}+\frac{{t}^{2}}{{λ}^{2}}=9$,
∴点M的轨迹方程C为:$\frac{{x}^{2}}{9}+\frac{{y}^{2}}{9{λ}^{2}}=1$(0<λ<1)
(2)由(1)得曲线C的右焦点为(3$\sqrt{1-{λ}^{2}}$,0)
斜率为1的直线lAB与的方程为:y=x-3$\sqrt{1-{λ}^{2}}$
设E(x1,y1),F(x2,y2),H(x0,y0),
假设在曲线C上存在点H使得△EFH的重心为坐标原点,则x0=-(x1+x2),y0=-(y1+y2),
联立$\left\{\begin{array}{l}{y=x-3\sqrt{1-{λ}^{2}}}\\{{λ}^{2}{x}^{2}+{y}^{2}=9{λ}^{2}}\end{array}\right.$得(${(λ}^{2}+1){x}^{2}-6\sqrt{1-{λ}^{2}}x+9-18{λ}^{2}=0$;
x1+x2=$\frac{6\sqrt{1-{λ}^{2}}}{{λ}^{2}+1}$,y1+y2=$\frac{-6{λ}^{2}\sqrt{1-{λ}^{2}}}{1+{λ}^{2}}$,
,H($\frac{6\sqrt{1-{λ}^{2}}}{1+{λ}^{2}},\frac{-6{λ}^{2}\sqrt{1-{λ}^{2}}}{1+{λ}^{2}}$)在曲线C上,
∴${λ}^{2}\frac{36(1-{λ}^{2})}{(1+{λ}^{2})^{2}}+\frac{36{λ}^{4}(1-{λ}^{2})}{(1+{λ}^{2})^{2}}=9{λ}^{2}$,
⇒λ2=$\frac{3}{5}$,∵0<λ<1.
∴在曲线C上存在点H使得△EFH的重心为坐标原点,此时$λ=\frac{\sqrt{15}}{5}$.
点评 本题考查了轨迹方程的求解,及圆锥曲线中的存在问题,属于中档题.

 星级口算天天练系列答案
星级口算天天练系列答案| A. | $\frac{4}{3}$ | B. | $\frac{5}{3}$ | C. | 2 | D. | 3 |
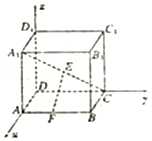 如图所示,在空间直角坐标系中,D是坐标原点,有一棱长为a的正方体ABCD-A1B1C1D1,E和F分别是体对角线A1C和棱AB上的动点,则|EF|的最小值为( )
如图所示,在空间直角坐标系中,D是坐标原点,有一棱长为a的正方体ABCD-A1B1C1D1,E和F分别是体对角线A1C和棱AB上的动点,则|EF|的最小值为( )| A. | $\sqrt{2}a$ | B. | $\frac{{\sqrt{2}}}{2}a$ | C. | a | D. | $\frac{1}{2}a$ |