题目内容
8.设函数f(x)=|x+1|(1)求不等式f(x)<2x的解集;
(2)若2f(x)+|x-a|>8对任意x∈R恒成立,求实数a的取值范围.
分析 (1)去掉绝对值号,得到关于x的不等式组,解出即可;(2)问题转化为f(x)+|x-a|>3对任意x∈R恒成立,即|a+1|>3,解出即可.
解答 解:(1)由f(x)<2x,得:|x+1|<2x,
则-2x<x+1<2x,
即$\left\{\begin{array}{l}{x+1<2x}\\{x+1>-2x}\end{array}\right.$,解得:x>1,
故不等式的解集是(1,+∞);
(2)∵f(x)+|x-a|=|x+1|+|x-a|≥|x+1-x+a|=|a+1|,
又2f(x)+|x-a|>8=23对任意x∈R恒成立,
即f(x)+|x-a|>3对任意x∈R恒成立,
∴|a+1|>3,解得:a>2或a<-4,
故a的范围是(-∞,-4)∪(2,+∞).
点评 本题考查了解绝对值不等式问题,考查绝对值的性质,是一道中档题.

练习册系列答案
相关题目
1.下列四组函数中,表示同一函数的是( )
| A. | f(x)=x0与g(x)=1 | B. | f(x)=x与g(x)=$\frac{{x}^{2}}{x}$ | ||
| C. | f(x)=x2-1与g(x)=x2+1 | D. | f(x)=|x|与g(x)=$\sqrt{{x}^{2}}$ |
16.将函数y=sinπx的图象沿x轴伸长到横坐标为原来的2倍,再向左平移1个单位,得到的图象对应的解析式是( )
| A. | $y=sin(\frac{πx}{2}+1)$ | B. | y=sin(2πx+1) | C. | $y=cos\frac{πx}{2}$ | D. | $y=-cos\frac{πx}{2}$ |
3.已知双曲线C:$\frac{{x}^{2}}{{a}^{2}}-\frac{{y}^{2}}{{b}^{2}}$=1(a>0,b>0)的左、右焦点分别为F1(-c,0),F2(c,0),P是双曲线C右支上一点,且|PF2|=|F1F2|.若直线PF1与圆x2+y2=a2相切,则双曲线的离心率为( )
| A. | $\frac{4}{3}$ | B. | $\frac{5}{3}$ | C. | 2 | D. | 3 |
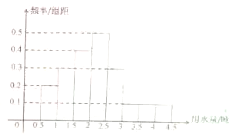 某城市100户居民的月平均用水量(单位:吨),按[0.5,1),[1,1.5),[1.5,2),[2,2.5),[2.5,3),[3,3.5),[3.5,4),[4,4.5)分组的频率分布直方图如图.
某城市100户居民的月平均用水量(单位:吨),按[0.5,1),[1,1.5),[1.5,2),[2,2.5),[2.5,3),[3,3.5),[3.5,4),[4,4.5)分组的频率分布直方图如图.