题目内容
11.已知a,b,c,分别为△ABC的内角A,B,C的对边,sin2B=2sinAsinC.(Ⅰ)若a=b=2,求cosB;
(Ⅱ)设B=90°,且$a=\sqrt{2}$,求△ABC的面积.
分析 (I)sin2B=2sinAsinC,由正弦定理可得:b2=2ac,再利用余弦定理即可得出.
(II)利用(I)及勾股定理可得c,再利用三角形面积计算公式即可得出.
解答 解:(I)∵sin2B=2sinAsinC,
∴由正弦定理$\frac{a}{sinA}=\frac{b}{sinB}=\frac{c}{sinC}$,可得:b2=2ac,
∵a=b=2,
∴c=1,
由余弦定理可得:cosB=$\frac{{a}^{2}+{c}^{2}-{b}^{2}}{2ac}$=$\frac{{2}^{2}+{1}^{2}-{2}^{2}}{2×2×1}$=$\frac{1}{4}$.
(II)由(I)可得:b2=2ac,
∵B=90°,且a=$\sqrt{2}$,
∴a2+c2=b2=2ac,解得a=c=$\sqrt{2}$.
∴S△ABC=$\frac{1}{2}$ac=1.
点评 本题考查了正弦定理余弦定理、勾股定理、三角形面积计算公式,考查了推理能力与计算能力,属于中档题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
4.在长方体ABCD-A1B1C1D1中,若$\overrightarrow{AB}$=$\overrightarrow{a}$,$\overrightarrow{AD}$=$\overrightarrow{b}$,$\overrightarrow{A{A}_{1}}$=$\overrightarrow{c}$,则$\overrightarrow{A{C}_{1}}$=( )
| A. | $\overrightarrow{a}$+$\overrightarrow{b}$-$\overrightarrow{c}$ | B. | $\overrightarrow{a}$-$\overrightarrow{b}$+$\overrightarrow{c}$ | C. | $\overrightarrow{a}$+$\overrightarrow{b}$+$\overrightarrow{c}$ | D. | -$\overrightarrow{a}$+$\overrightarrow{b}$+$\overrightarrow{c}$ |
2.等比数列{an}中,a2=4,a6和a2的等比中项等于±6,则a6=( )
| A. | 9 | B. | -9 | C. | ±8 | D. | 8 |
16.将函数y=sinπx的图象沿x轴伸长到横坐标为原来的2倍,再向左平移1个单位,得到的图象对应的解析式是( )
| A. | $y=sin(\frac{πx}{2}+1)$ | B. | y=sin(2πx+1) | C. | $y=cos\frac{πx}{2}$ | D. | $y=-cos\frac{πx}{2}$ |
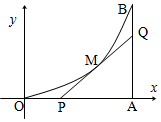 如图,由y=0,x=8,y=x2围成的曲边三角形,在曲线OB弧上求一点M,使得过M所作的y=x2的切线PQ与OA,AB围城的三角形PQA的面积最大,并求得最大值.
如图,由y=0,x=8,y=x2围成的曲边三角形,在曲线OB弧上求一点M,使得过M所作的y=x2的切线PQ与OA,AB围城的三角形PQA的面积最大,并求得最大值.