题目内容
12．已知全集U={x|x≥-3}，集合A={y|y=x2+4x+5}，$B=\{x|y=\sqrt{1-{{log}_2}x}\}$，则（∁UA）∩B=（ ）| A． | [-3，2] | B． | [-3，1） | C． | （0，1） | D． | （0，2] |
分析 化简集合A、B，根据补集与交集的定义写出运算结果即可．
解答 解：全集U={x|x≥-3}，
集合A={y|y=x2+4x+5}={y|y=（x+2）2+1≥1}=[1，+∞），
$B=\{x|y=\sqrt{1-{{log}_2}x}\}$={x|1-log2x≥0}={x|0＜x≤2}=（0，2]；
则∁UA=[-3，1），
∴（∁UA）∩B=（0，1）．
故选：C．
点评 本题考查了集合的化简与运算问题，是基础题目．
练习册系列答案
开心蛙口算题卡系列答案
相关题目
2．等比数列{an}中，a2=4，a6和a2的等比中项等于±6，则a6=（ ）
| A． | 9 | B． | -9 | C． | ±8 | D． | 8 |
3．已知双曲线C：$\frac{{x}^{2}}{{a}^{2}}-\frac{{y}^{2}}{{b}^{2}}$=1（a＞0，b＞0）的左、右焦点分别为F1（-c，0），F2（c，0），P是双曲线C右支上一点，且|PF2|=|F1F2|．若直线PF1与圆x2+y2=a2相切，则双曲线的离心率为（ ）
| A． | $\frac{4}{3}$ | B． | $\frac{5}{3}$ | C． | 2 | D． | 3 |
7．
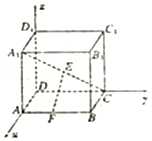如图所示，在空间直角坐标系中，D是坐标原点，有一棱长为a的正方体ABCD-A1B1C1D1，E和F分别是体对角线A1C和棱AB上的动点，则|EF|的最小值为（ ）
如图所示，在空间直角坐标系中，D是坐标原点，有一棱长为a的正方体ABCD-A1B1C1D1，E和F分别是体对角线A1C和棱AB上的动点，则|EF|的最小值为（ ）| A． | $\sqrt{2}a$ | B． | $\frac{{\sqrt{2}}}{2}a$ | C． | a | D． | $\frac{1}{2}a$ |
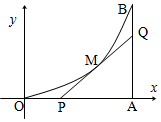如图，由y=0，x=8，y=x2围成的曲边三角形，在曲线OB弧上求一点M，使得过M所作的y=x2的切线PQ与OA，AB围城的三角形PQA的面积最大，并求得最大值．