题目内容
7．已知正数x，y满足x+y=1，则$\frac{4x+y}{xy}$的最小值为9．分析 把要求的式子变形为（x+y）（$\frac{1}{x}$+$\frac{4}{y}$），利用基本不等式即可得到$\frac{4x+y}{xy}$的最小值．
解答 解：∵正数x，y满足x+y=1，
∴$\frac{4x+y}{xy}$=$\frac{1}{x}$+$\frac{4}{y}$
=（x+y）（$\frac{1}{x}$+$\frac{4}{y}$）
=1+$\frac{4x}{y}$+$\frac{y}{x}$+4
≥5+2$\sqrt{4}$=9，
当且仅当$\frac{4x}{y}$=$\frac{y}{x}$时，取等号．
故答案为 9．
点评 本题考查基本不等式的应用，把要求的式子变形为（x+y）（$\frac{1}{x}$+$\frac{4}{y}$）=1+$\frac{4x}{y}$+$\frac{y}{x}$+4是解题的关键．
练习册系列答案
阅读快车系列答案
相关题目
5．已知函数f（x）=|2x-2|，方程f2（x）+tf（x）+1=0，（t∈R）有3个不同的实数根，则t的取值范围为（ ）
| A． | （-∞，-$\frac{5}{2}$] | B． | （-∞，-2] | C． | [-$\frac{5}{2}$，-2] | D． | [-2，+∞） |
6．已知向量$\overrightarrow{a}$=（cos$\frac{3}{2}$x，sin$\frac{3}{2}$x），$\overrightarrow{b}$=（cos$\frac{x}{2}$，-sin$\frac{x}{2}$），函数f（x）=$\overrightarrow{a}•\overrightarrow{b}$，g（x）=|$\overrightarrow{a}+\overrightarrow{b}$|，则下列性质正确的是（ ）
| A． | 函数f（x）的最小正周期为2π | B． | 函数g（x）为奇函数 | ||
| C． | 函数f（x）在[0．π]递减 | D． | 函数g（x）的最大值为2 |
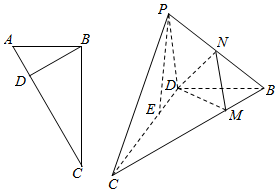如图，直角三角形ABC中，A=60°，沿斜边AC上的高BD，将△ABD折起到△PBD的位置，点E在线段CD上．
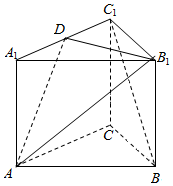已知三棱柱ABC-A1B1C1，△ABC是正三角形，直线AA1⊥平面A1B1C1，D是棱A1C1的中点．