题目内容
19．数列{an}的各项都是正数，a1=2，an+12=an2+2，那么此数列的通项公式为an=$\sqrt{2n+2}$．分析 a1=2，an+12=an2+2，即an+12-an2=2，可得：数列$\{{a}_{n}^{2}\}$是等差数列，利用等差数列的通项公式即可得出．
解答 解：∵a1=2，an+12=an2+2，即an+12-an2=2，
∴数列$\{{a}_{n}^{2}\}$是等差数列，公差为2，首项为4．
∴${a}_{n}^{2}$=4+2（n-1）=2n+2，an＞0，
∴an=$\sqrt{2n+2}$．
故答案为：$\sqrt{2n+2}$．
点评 本题考查了等差数列的通项公式，考查了推理能力与计算能力，属于中档题．
练习册系列答案
夺冠训练单元期末冲刺100分系列答案
新思维小冠军100分作业本系列答案
名师指导一卷通系列答案
相关题目
4．设m，n是不同的直线，α、β、γ是三个不同的平面，有以下四个命题：
①若m⊥α，n⊥α，则m∥n；
②若α∩γ=m，β∩γ=n，m∥n则α∥β；
③若α∥β，β∥γ，m⊥α，则m⊥γ
④若γ⊥α，γ⊥β，则α∥β．
其中正确命题的序号是（ ）
①若m⊥α，n⊥α，则m∥n；
②若α∩γ=m，β∩γ=n，m∥n则α∥β；
③若α∥β，β∥γ，m⊥α，则m⊥γ
④若γ⊥α，γ⊥β，则α∥β．
其中正确命题的序号是（ ）
| A． | ①③ | B． | ②③ | C． | ③④ | D． | ①④ |
11．方程$\frac{x^2}{2+m}+\frac{y^2}{m+1}$=1表示双曲线，则m的取值范围是（ ）
| A． | （-2，-1） | B． | （-2，+∞） | C． | （-∞，-1） | D． | （-∞，-2）∪（-1，+∞） |
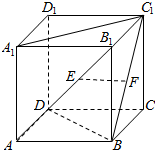如图，在正方体ABCD-A1B1C1D1中，E，F分别是AB1，BC1的中点，则以下结论中不成立的是③．（填序号）
9．设集合M={x|y=$\sqrt{{{log}_2}x-1}$}，N={x||x-1|≤2}，则M∩N=（ ）
| A． | [2，+∞） | B． | [-1，3] | C． | [2，3] | D． | [-1，2] |