题目内容
17.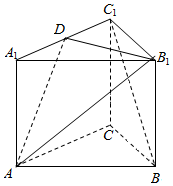 已知三棱柱ABC-A1B1C1,△ABC是正三角形,直线AA1⊥平面A1B1C1,D是棱A1C1的中点.
已知三棱柱ABC-A1B1C1,△ABC是正三角形,直线AA1⊥平面A1B1C1,D是棱A1C1的中点.(1)求证:B1D⊥平面AA1C1C;
(2)求证:BC1∥平面AB1D.
分析 (1)欲证明B1D⊥平面AA1C1C,只需推知B1D⊥A1C1,B1D⊥C1C1即可;
(2)连接A1B交AB1于点O,连接OD,欲证明BC1∥平面AB1D,只需推知BC1∥OD即可.
解答  证明:(1)∵在三棱柱ABC-A1B1C1中,△ABC是正三角形,
证明:(1)∵在三棱柱ABC-A1B1C1中,△ABC是正三角形,
∴△A1B1C1是正三角形,
又∵D是棱A1C1的中点,
∴B1D⊥A1C1.
∵AA1∥CC1,AA1⊥平面A1B1C1,
∴CC1⊥平面A1B1C1,B1D?平面A1B1C1,
∴CC1⊥B1D,
∵CC1∩AC1=C1,
∴B1D⊥平面AA1C1C.
(2)连接A1B交AB1于点O,连接OD,则O为BA1的中点.
∵D是棱A1C1的中点,
∴OD为△A1BC1的中位线.
∴OD∥BC1.
又OD?平面AB1D,BC1?面AB1D,
∴BC1∥平面AB1D.
点评 本题考查的知识是直线与平面垂直的判定,直线与平面平行的判定,其中熟练掌握空间直线与平面垂直及平行的判定、性质、定义、几何特征,及直三棱柱的几何特征,是解答本题的关键.

练习册系列答案
相关题目
5.若实数x,y满足约束条件$\left\{\begin{array}{l}{x-y-2≤0}\\{x+2y-7≥0}\\{y-3≤0}\end{array}\right.$,则z=$\frac{y}{x+1}$的最大值为( )
| A. | $\frac{3}{2}$ | B. | 1 | C. | $\frac{1}{2}$ | D. | $\frac{5}{14}$ |
12.若一个边长为a的正三角形,以其中一条高作为轴旋转,则所得旋转体的表面积为( )
| A. | $\frac{1}{4}$πa2 | B. | $\frac{1}{2}$πa2 | C. | $\frac{3}{4}$πa2 | D. | $\frac{1}{8}$πa2 |
9.设集合M={x|y=$\sqrt{{{log}_2}x-1}$},N={x||x-1|≤2},则M∩N=( )
| A. | [2,+∞) | B. | [-1,3] | C. | [2,3] | D. | [-1,2] |
6.复数($\frac{1+i}{1-i}$)3的模是( )
| A. | $\frac{1}{3}$ | B. | $\frac{1}{2}$ | C. | 1 | D. | 2 |
7.为了研究钟表与三角函数的关系,以9点与3点所在直线为x轴,以6点与12点为y轴,设秒针针尖指向位置P(x,y),若初始位置为P0($\frac{1}{2}$,$\frac{\sqrt{3}}{2}$),秒针从P0(注此时t=0)开始沿顺时针方向走动,则点P的纵坐标y与时间t(秒)的函数关系为( )
| A. | y=sin($\frac{π}{30}$t+$\frac{π}{3}$) | B. | y=sin($\frac{π}{30}$t-$\frac{π}{3}$) | C. | y=sin(-$\frac{π}{30}$t+$\frac{π}{3}$) | D. | y=sin(-$\frac{π}{30}$t-$\frac{π}{3}$) |
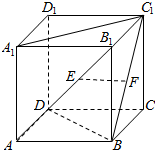 如图,在正方体ABCD-A1B1C1D1中,E,F分别是AB1,BC1的中点,则以下结论中不成立的是③.(填序号)
如图,在正方体ABCD-A1B1C1D1中,E,F分别是AB1,BC1的中点,则以下结论中不成立的是③.(填序号)