题目内容
6.已知向量$\overrightarrow{a}$=(cos$\frac{3}{2}$x,sin$\frac{3}{2}$x),$\overrightarrow{b}$=(cos$\frac{x}{2}$,-sin$\frac{x}{2}$),函数f(x)=$\overrightarrow{a}•\overrightarrow{b}$,g(x)=|$\overrightarrow{a}+\overrightarrow{b}$|,则下列性质正确的是( )| A. | 函数f(x)的最小正周期为2π | B. | 函数g(x)为奇函数 | ||
| C. | 函数f(x)在[0.π]递减 | D. | 函数g(x)的最大值为2 |
分析 利用三角函数的恒等变换和向量的数量积公式求出f(x)和g(x)的解析式,利用余弦函数的性质进行判断.
解答 解:f(x)=$\overrightarrow{a}•\overrightarrow{b}$=cos$\frac{3}{2}$xcos$\frac{x}{2}$-sin$\frac{3}{2}$xsin$\frac{x}{2}$=cos2x,
∴f(x)的最小正周期为$\frac{2π}{2}$=π,故A错误.
∵f(0)=1,f(π)=1,∴f(x)在[0,π]上不单调,故C错误.
∵$\overrightarrow{a}+\overrightarrow{b}$=(cos$\frac{3}{2}$x+cos$\frac{x}{2}$,sin$\frac{3}{2}$x-sin$\frac{x}{2}$),
∴($\overrightarrow{a}+\overrightarrow{b}$)2=(cos$\frac{3}{2}$x+cos$\frac{x}{2}$)2+(sin$\frac{3}{2}$x-sin$\frac{x}{2}$)2=2+2cos$\frac{3}{2}$xcos$\frac{x}{2}$-2sin$\frac{3}{2}$xsin$\frac{x}{2}$=2+2cos2x.
∴g(x)=$\sqrt{2+2cos2x}$,
∴g(x)是偶函数,故B错误.
当cos2x=1时,g(x)取得最大值2.故D正确.
故选:D.
点评 本题考查了平面向量的数量积运算,三角函数的恒等变换,余弦函数的图象与性质,属于中档题.

练习册系列答案
 初中学业考试导与练系列答案
初中学业考试导与练系列答案
相关题目
16.设f(x)是R上的偶函数,并且在[0,+∞)上单调递减,则f(-1),f(-3),f(5)的大小顺序是( )
| A. | f(-1)>f(-3)>f(5) | B. | f(-1)>f(5)>f(-3) | C. | f(5)>f(-1)>f(-3) | D. | f(-3)>f(-1)>f(5) |
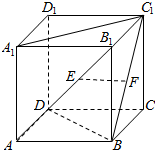 如图,在正方体ABCD-A1B1C1D1中,E,F分别是AB1,BC1的中点,则以下结论中不成立的是③.(填序号)
如图,在正方体ABCD-A1B1C1D1中,E,F分别是AB1,BC1的中点,则以下结论中不成立的是③.(填序号)