题目内容
5.已知函数f(x)=|2x-2|,方程f2(x)+tf(x)+1=0,(t∈R)有3个不同的实数根,则t的取值范围为( )| A. | (-∞,-$\frac{5}{2}$] | B. | (-∞,-2] | C. | [-$\frac{5}{2}$,-2] | D. | [-2,+∞) |
分析 由题意作函数f(x)=|2x-2|的图象,从而分类讨论求方程的根的个数.
解答 解:由题意作函数f(x)=|2x-2|的图象如下,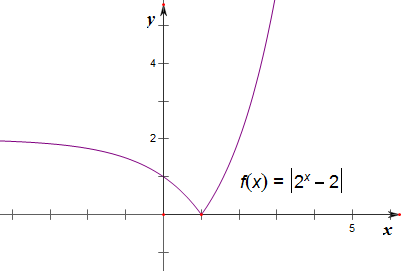 ,
,
当f(x)=2时,代入可得4+2t+1=0,
解得,t=-$\frac{5}{2}$,
此时,f2(x)+tf(x)+1=0的两根为:
f(x)=2或f(x)=$\frac{1}{2}$,
故f2(x)+tf(x)+1=0有三个不同的根;
当4+2t+1<0,即t<$\frac{5}{2}$时,
方程f2(x)+tf(x)+1=0有三个不同的根;
故t的取值范围为(-∞,-$\frac{5}{2}$].
故选:A.
点评 本题考查了函数的零点与方程的根的关系应用及数形结合的思想方法应用,属于中档题.

练习册系列答案
相关题目
16.设f(x)是R上的偶函数,并且在[0,+∞)上单调递减,则f(-1),f(-3),f(5)的大小顺序是( )
| A. | f(-1)>f(-3)>f(5) | B. | f(-1)>f(5)>f(-3) | C. | f(5)>f(-1)>f(-3) | D. | f(-3)>f(-1)>f(5) |
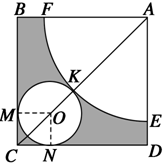 如图所示,在边长为$5+\sqrt{2}$的正方形ABCD中,以A为圆心画一个扇形,以O为圆心画一个圆,M,N,K为切点,以扇形为圆锥的侧面,以圆O为圆锥底面,围成一个圆锥,求圆锥的表面积与体积.
如图所示,在边长为$5+\sqrt{2}$的正方形ABCD中,以A为圆心画一个扇形,以O为圆心画一个圆,M,N,K为切点,以扇形为圆锥的侧面,以圆O为圆锥底面,围成一个圆锥,求圆锥的表面积与体积.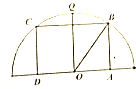 如图,四边形ABCD是半径为1的半圆O的内接矩形,其中A、D在直径上,Q为弧CB的中点,设∠BOQ=θ,记f(θ)=$\frac{1}{OA}$+$\frac{1}{AB}$,求f(θ)的最小值.
如图,四边形ABCD是半径为1的半圆O的内接矩形,其中A、D在直径上,Q为弧CB的中点,设∠BOQ=θ,记f(θ)=$\frac{1}{OA}$+$\frac{1}{AB}$,求f(θ)的最小值.