题目内容
已知函数f（x）=|x|（a-x），a∈R．
（1）若函数f（x）在x∈[0，2]上是单调函数，求实数a的取值范围．
（2）对于确定的正数b，不等式|x|（a-x）≤b，对x∈[-1，2]恒成立，求实数a的取值范围．
（1）若函数f（x）在x∈[0，2]上是单调函数，求实数a的取值范围．
（2）对于确定的正数b，不等式|x|（a-x）≤b，对x∈[-1，2]恒成立，求实数a的取值范围．
考点：函数恒成立问题
专题：函数的性质及应用
分析：（1）当x∈[0，2]时，该函数化为y=-x2+ax，结合其图象可知，只要对称轴在区间[0，2]的外侧即可；
（2）先将不等式化成a≤x+
，再分x∈[-1，0]和[0，2]两种情况求出y=x+
的最小值，综合得到整个定义域上的最小值，只需a小于或等于其最小值即可．
（2）先将不等式化成a≤x+
| b |
| |x| |
| b |
| |x| |
解答：
解：（1）由题意原函数化为f（x）=-x2+ax，该函数图象开口向下，对称轴为x=
，
故其在（-∞，
）递增，在[
，+∞）上递减，所以要使函数在x∈[0，2]上是单调函数，
只需
≤0或
≥2，解得a≤0或a≥4，
即a的范围是a≤0或a≥4．
（2）由题意①x=0时，b≥0显然成立，此时a∈R，
②当x≠0时，原式可化为：a≤x+
，x∈[-1，2]恒成立，
若x∈[-1，0），则a≤x-
，函数y=x-
在[-1，0）上是增函数，所以只需a≤（x-
）min=-1+b；
若x∈（0，2]，则a≤x+
，函数y=x+
在（0，
）递减，在[
，+∞）上递增，
因此若
≥2，即b≥4时，y=x+
在（0，2]递减，所以a≤（x+
）min=2+
，
若
＜2，即0＜b＜4时，y=x+
在（0，
]上递减，在（
，2]上递增，此时a≤(x+
)min=2
综合①②可知当b≥4时，y=x+
在[-1，2]的最小值为b-1，所以此时a≤b-1；
当0＜b＜4时，b-1-2
=（
-1）2-2＜0恒成立，所以此时函数y=x+
在[-1，2]的最小值也是b-1，故a≤b-1；
因此a≤b-1即为所求．
| a |
| 2 |
故其在（-∞，
| a |
| 2 |
| a |
| 2 |
只需
| a |
| 2 |
| a |
| 2 |
即a的范围是a≤0或a≥4．
（2）由题意①x=0时，b≥0显然成立，此时a∈R，
②当x≠0时，原式可化为：a≤x+
| b |
| |x| |
若x∈[-1，0），则a≤x-
| b |
| x |
| b |
| x |
| b |
| x |
若x∈（0，2]，则a≤x+
| b |
| x |
| b |
| x |
| b |
| b |
因此若
| b |
| b |
| x |
| b |
| x |
| b |
| 2 |
若
| b |
| b |
| x |
| b |
| b |
| b |
| x |
| b |
综合①②可知当b≥4时，y=x+
| b |
| |x| |
当0＜b＜4时，b-1-2
| b |
| b |
| b |
| |x| |
因此a≤b-1即为所求．
点评：本题难度较大，先将不等式合理转化为a≤x+
，x∈[-1，2]恒成立，是解题的关键；再就是准确理解在整个区间上求出函数在x∈[-1，2]上的最小值，先分段来求，最后综合比较，小中取小．
| b |
| |x| |
练习册系列答案
一诺书业暑假作业快乐假期云南美术出版社系列答案
相关题目
已知△ABC是边长为2的正三角形，则它的平面直观图△A′B′C′的面积为（ ）
A、
| ||||
B、
| ||||
C、
| ||||
D、
|
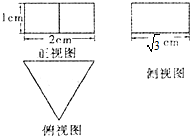某个几何体的三视图如图所示，其中俯视图为等边三角形，则该几何体的表面积是（ ）A、
| ||
B、6+
| ||
C、6+2
| ||
D、6+3
|