题目内容
10.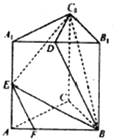 在三棱柱ABC-A1B1C1中,AB=BC=CA=AA1=2,侧棱AA1⊥平面ABC,且D,E分别是棱A1B1,A1A1的中点,点F在棱AB上,且AF=$\frac{1}{4}$AB.
在三棱柱ABC-A1B1C1中,AB=BC=CA=AA1=2,侧棱AA1⊥平面ABC,且D,E分别是棱A1B1,A1A1的中点,点F在棱AB上,且AF=$\frac{1}{4}$AB.(1)求证:EF∥平面BDC1;
(2)求三棱锥D-BEC1的体积.
分析 (1)取AB的中点O,连接A1O,利用中位线定理得EF∥A1O,由四边形A1DBO为平行四边形得出A${\;}_{{\;}_{1}}$O∥BD,故而EF∥BD,于是EF∥平面BDC1;
(2)证明C1D⊥平面AA1B1B,于是V${\;}_{D-BE{C}_{1}}$=V${\;}_{{C}_{1}-BDE}$=$\frac{1}{3}{S}_{△BDE}•{C}_{1}D$.
解答  解:(1)取AB的中点O,连接A1O,
解:(1)取AB的中点O,连接A1O,
∵AF=$\frac{1}{4}$AB,
∴F为AO的中点,又E为AA1的中点,
∴EF∥A1O,
∵A1D=$\frac{1}{2}{A}_{1}{B}_{1}$,BO=$\frac{1}{2}AB$,AB$\stackrel{∥}{=}$A1B1,
∴A1D$\stackrel{∥}{=}BO$
∴四边形A1DBO为平行四边形,
∴A1O∥BD,
∴EF∥BD,又EF?平面BDC1,BD?平面BDC1,
∴EF∥平面BDC1.
(2)∵AA1⊥平面A1B1C1,C1D?平面A1B1C1,
∴AA1⊥C1D,
∵A1C1=B1C1=A1B1=2,D为A1B1的中点,
∴C1D⊥A1B1,C1D=$\sqrt{3}$,
又AA1?平面AA1B${\;}_{{\;}_{1}}$B,A1B1?平面AA1B${\;}_{{\;}_{1}}$B,AA1∩A1B1=A1,
∴C1D⊥平面AA1B1B,
∵AB=AA1=2,D,E分别为A1B1,AA1的中点,
∴S△BDE=22-$\frac{1}{2}×1×2$-$\frac{1}{2}×1×2$-$\frac{1}{2}×1×1$=$\frac{3}{2}$.
∴V${\;}_{D-BE{C}_{1}}$=V${\;}_{{C}_{1}-BDE}$=$\frac{1}{3}{S}_{△BDE}•{C}_{1}D$=$\frac{1}{3}×\frac{3}{2}×\sqrt{3}$=$\frac{\sqrt{3}}{2}$.
点评 本题考查了线面平行的判定,线面垂直的判定,棱锥的体积计算,属于中档题.

 阅读快车系列答案
阅读快车系列答案| A. | $[\frac{π}{4},\frac{3π}{4}]$ | B. | $[0,\frac{3π}{4}]$ | C. | $[-\frac{π}{4},\frac{π}{4}]$ | D. | $[0,\frac{π}{4}]∪[\frac{3π}{4},π)$ |
| A. | 坐标原点对称 | B. | x轴对称 | C. | y轴对称 | D. | 直线y=x |
| A. | -$\frac{1}{2}$ | B. | $\frac{1}{2}$ | C. | -$\frac{1}{4}$ | D. | $\frac{1}{4}$ |
| A. | 6π | B. | 4π | C. | 3π | D. | 12π |
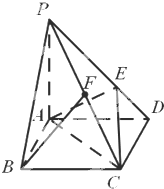 如图,在底面是菱形的四棱锥P-ABCD中,点E在PD上,且满足PE:ED=2:1,PA=AB=2,PA⊥底面ABCD,∠ABC=60°
如图,在底面是菱形的四棱锥P-ABCD中,点E在PD上,且满足PE:ED=2:1,PA=AB=2,PA⊥底面ABCD,∠ABC=60°