题目内容
20.若直线l的斜率k的取值范围为[-1,1],则其倾斜角α的取值范围是( )| A. | $[\frac{π}{4},\frac{3π}{4}]$ | B. | $[0,\frac{3π}{4}]$ | C. | $[-\frac{π}{4},\frac{π}{4}]$ | D. | $[0,\frac{π}{4}]∪[\frac{3π}{4},π)$ |
分析 由题意可得:-1≤tanα≤1,然后求解三角不等式得答案.
解答 解:设直线l的倾斜角为α(0≤α<π),
由题意知:-1≤tanα≤1,
解得:0$≤α≤\frac{π}{4}$或$\frac{3π}{4}≤α<π$.
∴倾斜角α的取值范围是[0,$\frac{π}{4}$]∪[$\frac{3π}{4},π$).
故选:D.
点评 本题考查直线的倾斜角,考查了直线倾斜角与斜率的关系,是基础题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
11.某种产品的广告费支出x(单位:百万元)与销售额y(单位:百万元)之间有如下对应数据:
$\widehatb=\frac{{\sum_{i=1}^n{({x_i}-\overline x)({y_i}-\overline y)}}}{{\sum_{i=1}^n{{{({x_i}-\overline x)}^2}}}}$,$\widehata=\overline y-\widehatb\overline x$
(1)求y关于x的回归直线方程.
(2)预测广告费支出为10(单位:百万元)时,销售额为多少?
| x | 2 | 4 | 5 | 6 | 8 |
| y | 30 | 40 | 60 | 50 | 70 |
(1)求y关于x的回归直线方程.
(2)预测广告费支出为10(单位:百万元)时,销售额为多少?
5.函数y=2sin($\frac{π}{6}$-2x)(其中x∈[-π,0])的单调递增区间是( )
| A. | $[{-π,-\frac{5π}{6}}]$ | B. | $[{-\frac{π}{3},0}]$ | C. | $[{-\frac{2π}{3},-\frac{π}{6}}]$ | D. | $[{-\frac{π}{3},-\frac{π}{6}}]$ |
12.曲线y=$\frac{ax}{x+2}$在点(-1,-a)处的切线方程为2x-y+b=0,则a+b=( )
| A. | 0 | B. | 2 | C. | -4 | D. | -3 |
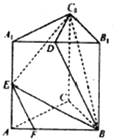 在三棱柱ABC-A1B1C1中,AB=BC=CA=AA1=2,侧棱AA1⊥平面ABC,且D,E分别是棱A1B1,A1A1的中点,点F在棱AB上,且AF=$\frac{1}{4}$AB.
在三棱柱ABC-A1B1C1中,AB=BC=CA=AA1=2,侧棱AA1⊥平面ABC,且D,E分别是棱A1B1,A1A1的中点,点F在棱AB上,且AF=$\frac{1}{4}$AB.