题目内容
15．已知f（x）的导函数为f'（x），满足xf'（x）+2f（x）=$\frac{1}{x}$，且f（1）=2，则f（x）的最小值为（ ）| A． | -$\frac{1}{2}$ | B． | $\frac{1}{2}$ | C． | -$\frac{1}{4}$ | D． | $\frac{1}{4}$ |
分析 把已知等式两边同时乘以x，得到[x2f（x）]′=1，令x2f（x）=x+c，由f（1）=2求得c值，则函数解析式可求，然后利用二次函数求最值．
解答 解：∵xf′（x）+2f（x）=$\frac{1}{x}$，
∴x2f′（x）+2xf（x）=1，
∴[x2f（x）]′=1，
∴x2f（x）=x+c，
将x=1代入可得：
f（1）=1+c=2，得c=1，
∴x2f（x）=x+1，
∴f（x）=$\frac{x+1}{{x}^{2}}=\frac{1}{{x}^{2}}+\frac{1}{x}$，
∴当$\frac{1}{x}=-\frac{1}{2}$，即x=-2时，$f（x）_{min}=-\frac{1}{4}$．
故选：C．
点评 本题考查的知识点是导数的运算，导数在求函数最值时的应用，关键是合理构造函数，是中档题．
练习册系列答案
相关题目
5．函数y=2sin（$\frac{π}{6}$-2x）（其中x∈[-π，0]）的单调递增区间是（ ）
| A． | $[{-π，-\frac{5π}{6}}]$ | B． | $[{-\frac{π}{3}，0}]$ | C． | $[{-\frac{2π}{3}，-\frac{π}{6}}]$ | D． | $[{-\frac{π}{3}，-\frac{π}{6}}]$ |
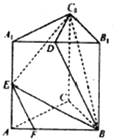在三棱柱ABC-A1B1C1中，AB=BC=CA=AA1=2，侧棱AA1⊥平面ABC，且D，E分别是棱A1B1，A1A1的中点，点F在棱AB上，且AF=$\frac{1}{4}$AB．
20．已知集合U={-1，0，1，2}，A={-1，2}，则∁UA=（ ）
| A． | {0} | B． | {1} | C． | {0，1} | D． | {-1，0，1} |
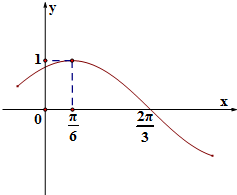已知函数f（x）=Asin（ωx+φ）（-$\frac{π}{2}$＜φ＜$\frac{π}{2}$，ω＞0，A＞0）其部分图象如图所示：
4．函数f（x）=log0.5（x2-4）的单调递增区间是（ ）
| A． | （-∞，0） | B． | （-∞，-2） | C． | （0，+∞） | D． | （2，+∞） |