题目内容
5.已知$\sqrt{2+\frac{2}{3}}$=2$\sqrt{\frac{2}{3}}$,$\sqrt{3+\frac{3}{8}}$=3$\sqrt{\frac{3}{8}}$,$\sqrt{4+\frac{4}{15}}$=4$\sqrt{\frac{4}{15}}$,…,依此规律,若$\sqrt{9+\frac{9}{m}}$=$9\sqrt{\frac{9}{m}}$,则m的值为80.分析 仔细观察已知等式的数字可发现$\sqrt{n+\frac{n}{{n}^{2}-1}}$=n$\sqrt{\frac{n}{{n}^{2}-1}}$,根据此规律解题即可.
解答 解:$\sqrt{2+\frac{2}{3}}$=2$\sqrt{\frac{2}{3}}$,
$\sqrt{3+\frac{3}{8}}$=3$\sqrt{\frac{3}{8}}$,
$\sqrt{4+\frac{4}{15}}$=4$\sqrt{\frac{4}{15}}$,
…,依此规律,
得到$\sqrt{n+\frac{n}{{n}^{2}-1}}$=n$\sqrt{\frac{n}{{n}^{2}-1}}$,
故m=92-1=80,
故答案为:80.
点评 本题是一道找规律的题目,要求学生通过观察,分析、归纳并发现其中的规律,并应用发现的规律解决问题.

练习册系列答案
 世纪百通优练测系列答案
世纪百通优练测系列答案 百分学生作业本题练王系列答案
百分学生作业本题练王系列答案
相关题目
13.某初级中学有学生270人,其中七年级108人,八、九年级各81人.现要利用抽样方法抽取10人参加某项调查,考虑用简单随机抽样、分层抽样和系统抽样三种方案.使用简单随机抽样和分层抽样时,学生按照七、八、九年级依次统一编号为1、2、3、…、270;使用系统抽样时,将学生统一随机编号为1、2、3、…、270,并将整个编号依次分为10段.如果抽得号码有下列四种情况:
①7、34、61、88、115、142、169、196、223、250
②5、9、100、107、111、121、180、190、200、265
③11、38、65、92、119、146、173、200、227、254
④30、57、84、111、138、165、192、219、246、270
关于上述样本的下列结论中,正确的是( )
①7、34、61、88、115、142、169、196、223、250
②5、9、100、107、111、121、180、190、200、265
③11、38、65、92、119、146、173、200、227、254
④30、57、84、111、138、165、192、219、246、270
关于上述样本的下列结论中,正确的是( )
| A. | ②③都不能为系统抽样 | B. | ②④都不能为分层抽样 | ||
| C. | ①④都可能为系统抽样 | D. | ①③都可能为分层抽样 |
17.废品率x%和每吨生铁成本y(元)之间的回归直线方程为y=256+2x,表明( )
| A. | 废品率每增加1%,生铁成本增加258元 | |
| B. | 废品率每增加1%,生铁成本增加2元 | |
| C. | 废品率每增加1%,生铁成本每吨增加2元 | |
| D. | 废品率不变,生铁成本为256元 |
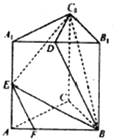 在三棱柱ABC-A1B1C1中,AB=BC=CA=AA1=2,侧棱AA1⊥平面ABC,且D,E分别是棱A1B1,A1A1的中点,点F在棱AB上,且AF=$\frac{1}{4}$AB.
在三棱柱ABC-A1B1C1中,AB=BC=CA=AA1=2,侧棱AA1⊥平面ABC,且D,E分别是棱A1B1,A1A1的中点,点F在棱AB上,且AF=$\frac{1}{4}$AB.