题目内容
18．若复数z满足z（1-i）=|1-i|+i，则$\overline{z}$的虚部为$-\frac{\sqrt{2}+1}{2}$．分析 把已知等式变形，利用复数代数形式的乘除运算化简，求得$\overline{z}$得答案．
解答 解：由z（1-i）=|1-i|+i，得$z=\frac{|1-i|+i}{1-i}=\frac{\sqrt{2}+i}{1-i}$=$\frac{（\sqrt{2}+i）（1+i）}{（1-i）（1+i）}=\frac{（\sqrt{2}-1）+（\sqrt{2}+1）i}{2}$．
∴$\overline{z}=\frac{\sqrt{2}-1}{2}-\frac{\sqrt{2}+1}{2}i$，
则$\overline{z}$的虚部为$-\frac{\sqrt{2}+1}{2}$．
故答案为：$-\frac{\sqrt{2}+1}{2}$．
点评 本题考查复数代数形式的乘除运算，考查了复数的基本概念，是基础题．
练习册系列答案
相关题目
13．某初级中学有学生270人，其中七年级108人，八、九年级各81人．现要利用抽样方法抽取10人参加某项调查，考虑用简单随机抽样、分层抽样和系统抽样三种方案．使用简单随机抽样和分层抽样时，学生按照七、八、九年级依次统一编号为1、2、3、…、270；使用系统抽样时，将学生统一随机编号为1、2、3、…、270，并将整个编号依次分为10段．如果抽得号码有下列四种情况：
①7、34、61、88、115、142、169、196、223、250
②5、9、100、107、111、121、180、190、200、265
③11、38、65、92、119、146、173、200、227、254
④30、57、84、111、138、165、192、219、246、270
关于上述样本的下列结论中，正确的是（ ）
①7、34、61、88、115、142、169、196、223、250
②5、9、100、107、111、121、180、190、200、265
③11、38、65、92、119、146、173、200、227、254
④30、57、84、111、138、165、192、219、246、270
关于上述样本的下列结论中，正确的是（ ）
| A． | ②③都不能为系统抽样 | B． | ②④都不能为分层抽样 | ||
| C． | ①④都可能为系统抽样 | D． | ①③都可能为分层抽样 |
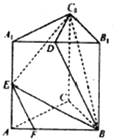在三棱柱ABC-A1B1C1中，AB=BC=CA=AA1=2，侧棱AA1⊥平面ABC，且D，E分别是棱A1B1，A1A1的中点，点F在棱AB上，且AF=$\frac{1}{4}$AB．
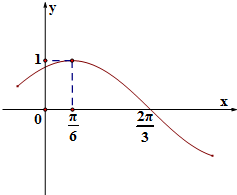已知函数f（x）=Asin（ωx+φ）（-$\frac{π}{2}$＜φ＜$\frac{π}{2}$，ω＞0，A＞0）其部分图象如图所示：
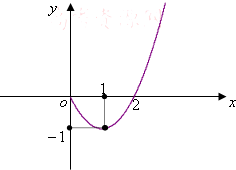已知二次函数y=f（x）在[0，+∞）上的图象如图所示，顶点坐标为（1，-1）．