题目内容
已知命题p:实数x满足x2-4ax+3a2<0(其中a≠0),命题q:实数x满足
≤0.
(1)若a=1,且p∧q为真,求实数x的取值范围;
(2)若p是q的必要不充分条件,求实数a的取值范围.
| x-3 |
| x-2 |
(1)若a=1,且p∧q为真,求实数x的取值范围;
(2)若p是q的必要不充分条件,求实数a的取值范围.
考点:复合命题的真假,必要条件、充分条件与充要条件的判断
专题:简易逻辑
分析:(1)若a=1,求出命题p,q的等价条件,利用p∧q为真,则p,q为真,即可求实数x的取值范围;
(2)求出命题p的等价条件,利用p是q的必要不充分条件,即可求实数a的取值范围.
(2)求出命题p的等价条件,利用p是q的必要不充分条件,即可求实数a的取值范围.
解答:
解:(1)若a=1,不等式为x2-4x+3<0,即1<x<3,即p:1<x<3,
若
≤0,则2<x≤3,即q:2<x≤3,
若p∧q为真,则p,q同时为真,
即
,解得2<x<3,
则实数x的取值范围是2<x<3;
(2)∵x2-4ax+3a2<0,
∴(x-a)(x-3a)<0,
若a>0,则不等式的解为a<x<3a,
若a<0,则不等式的解为3a<x<a,
∵q:2<x≤3,
∴若p是q的必要不充分条件,
则a>0,且
,
即1<a≤2,
则实数a的取值范围是1<a≤2.
若
| x-3 |
| x-2 |
若p∧q为真,则p,q同时为真,
即
|
则实数x的取值范围是2<x<3;
(2)∵x2-4ax+3a2<0,
∴(x-a)(x-3a)<0,
若a>0,则不等式的解为a<x<3a,
若a<0,则不等式的解为3a<x<a,
∵q:2<x≤3,
∴若p是q的必要不充分条件,
则a>0,且
|
即1<a≤2,
则实数a的取值范围是1<a≤2.
点评:本题主要考查充分条件和必要条件的应用,以及不等式的求解,利用不等式的解法时解决本题的关键.

练习册系列答案
相关题目
已知数列a1=2中,a1=2,an+1=an+
(n∈N*),则a101的值( )
| 1 |
| 2 |
| A、50 | B、51 | C、52 | D、53 |
已知α为锐角,且sin(α-
)=
,则sinα=( )
| π |
| 4 |
| 1 |
| 3 |
A、
| ||||
B、
| ||||
C、
| ||||
D、
|
利用基本不等式求最值,下列各式运用正确的是( )
A、y=x+
| ||||||
B、y=sinx+
| ||||||
C、y=3x+
| ||||||
D、y=lgx+4logx10≥2
|
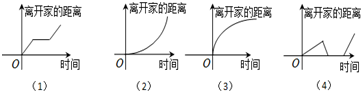
下列所给4个图象中,与所给3件事吻合最好的顺序为( )
(1)我离开家不久,发现自己把作业本忘在家里了,于是立刻返回家里取了作业本再上学;
(2)我骑着车一路以常速行驶,只是在途中遇到一次交通堵塞,耽搁了一些时间;
(3)我出发后,心情轻松,缓缓行进,后来为了赶时间开始加速.
(1)(2)(3)(4)时间时间时间时间离开家的距离离开家的距离离开家的距离离开家的距离
(1)我离开家不久,发现自己把作业本忘在家里了,于是立刻返回家里取了作业本再上学;
(2)我骑着车一路以常速行驶,只是在途中遇到一次交通堵塞,耽搁了一些时间;
(3)我出发后,心情轻松,缓缓行进,后来为了赶时间开始加速.
(1)(2)(3)(4)时间时间时间时间离开家的距离离开家的距离离开家的距离离开家的距离

| A、(1)(2)(4) |
| B、(4)(2)(3) |
| C、(4)(1)(3) |
| D、(4)(1)(2) |
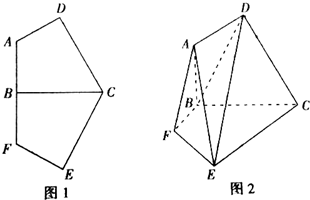 已知平面内有一个五边形ABCEF,且关于线段BC对称(如图1所示),FE⊥CE,BF=FE=1,CB=CE=
已知平面内有一个五边形ABCEF,且关于线段BC对称(如图1所示),FE⊥CE,BF=FE=1,CB=CE=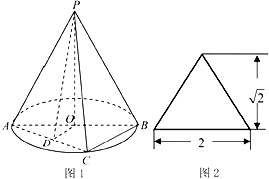 圆锥PO如图1所示,图2是它的正(主)视图.已知圆O的直径为AB,C是圆周上异于A、B的一点,D为AC的中点
圆锥PO如图1所示,图2是它的正(主)视图.已知圆O的直径为AB,C是圆周上异于A、B的一点,D为AC的中点 已知函数f(x)=2cos2(
已知函数f(x)=2cos2(