题目内容
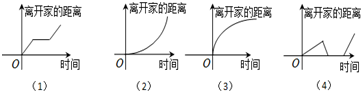
下列所给4个图象中,与所给3件事吻合最好的顺序为( )
(1)我离开家不久,发现自己把作业本忘在家里了,于是立刻返回家里取了作业本再上学;
(2)我骑着车一路以常速行驶,只是在途中遇到一次交通堵塞,耽搁了一些时间;
(3)我出发后,心情轻松,缓缓行进,后来为了赶时间开始加速.
(1)(2)(3)(4)时间时间时间时间离开家的距离离开家的距离离开家的距离离开家的距离
(1)我离开家不久,发现自己把作业本忘在家里了,于是立刻返回家里取了作业本再上学;
(2)我骑着车一路以常速行驶,只是在途中遇到一次交通堵塞,耽搁了一些时间;
(3)我出发后,心情轻松,缓缓行进,后来为了赶时间开始加速.
(1)(2)(3)(4)时间时间时间时间离开家的距离离开家的距离离开家的距离离开家的距离

| A、(1)(2)(4) |
| B、(4)(2)(3) |
| C、(4)(1)(3) |
| D、(4)(1)(2) |
考点:函数的图象
专题:函数的性质及应用
分析:根据回家后,离家的距离又变为0,可判断(1)的图象开始后不久又回归为0;由途中遇到一次交通堵塞,可判断中间有一段函数值没有发生变化;由为了赶时间开始加速,可判断函数的图象上升速度越来越快.
解答:
解:离家不久发现自己作业本忘记在家里,回到家里,这时离家的距离为0,故应先选图象④;
回校途中有一段时间交通堵塞,则这段时间与家的距离必为一定值,故应选图象①;
最后加速向学校,其距离与时间的关系为二次函数,故应选图象②.
故选:D.
回校途中有一段时间交通堵塞,则这段时间与家的距离必为一定值,故应选图象①;
最后加速向学校,其距离与时间的关系为二次函数,故应选图象②.
故选:D.
点评:本题考查的知识点是函数的图象,我们分析实际情况中离家距离随时间变化的趋势,找出关键的图象特征,对四个图象进行分析,即可得到答案.

练习册系列答案
 备战中考寒假系列答案
备战中考寒假系列答案
相关题目
如图是由一些火柴棒拼成的一系列图形,如第1个图中有4根火柴棒,第2个图中有7根火柴棒,则在第51个图中有火柴棒( )


| A、150根 | B、153根 |
| C、154根 | D、156根 |
已知等差数列{an}的首项为a,公差为d,且方程ax2-3x+2=0的解为1和d,则数列{3n-1an}的前n项和Tn为( )
| A、3n |
| B、1+(n-1)3n |
| C、n•3n |
| D、1+(n+1)•3n |
若a<b<0,那么下列不等式中正确的是( )
A、
| ||||
B、
| ||||
| C、ab<b2 | ||||
| D、ab>a2 |
已知数列{an}为等比数列,且a1=1,a4=8,则公比q=( )
| A、1 | B、2 | C、4 | D、8 |