题目内容
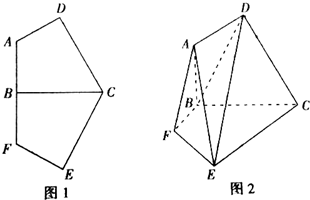 已知平面内有一个五边形ABCEF,且关于线段BC对称(如图1所示),FE⊥CE,BF=FE=1,CB=CE=
已知平面内有一个五边形ABCEF,且关于线段BC对称(如图1所示),FE⊥CE,BF=FE=1,CB=CE=| 3 |
(1)证明:DE∥平面AFB;
(2)求二面角E-AD-B的余弦值.
考点:与二面角有关的立体几何综合题,直线与平面平行的判定
专题:空间位置关系与距离,空间角
分析:几何法:
(1)作DQ∥AB交BC于点Q,连接EQ.由已知条件得EQ∥FB.所以DQ∥面AFB.同理:EQ∥面AFB.由此能证明DE∥平面AFB.
(2)延长DA、CB、EF,必交于一点G,过点B作BH⊥DG于点H,连接HF.由已知条件得∠BHF是二面角E-AD-B的平面角.由此能求出二面角E-AD-B的余弦值.
向量法:
(1)B为坐标原点,建立空间直角坐标系,利用向量法能证明DE∥平面AFB.
(2)分别求出平面ADEF的一个法向量和面ABCD的一个法向量,由此能求出二面角E-AD-B的余弦值.
(1)作DQ∥AB交BC于点Q,连接EQ.由已知条件得EQ∥FB.所以DQ∥面AFB.同理:EQ∥面AFB.由此能证明DE∥平面AFB.
(2)延长DA、CB、EF,必交于一点G,过点B作BH⊥DG于点H,连接HF.由已知条件得∠BHF是二面角E-AD-B的平面角.由此能求出二面角E-AD-B的余弦值.
向量法:
(1)B为坐标原点,建立空间直角坐标系,利用向量法能证明DE∥平面AFB.
(2)分别求出平面ADEF的一个法向量和面ABCD的一个法向量,由此能求出二面角E-AD-B的余弦值.
解答:
几何法:
(1)证明:如图,作DQ∥AB交BC于点Q,连接EQ.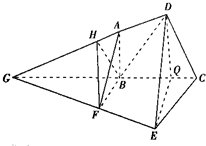
∵五边形ABCEF关于线段BC对称,
∴EQ∥FB.
又DQ?面ABF,AB?面ABF,
∴DQ∥面AFB.同理:EQ∥面AFB.
又DQ∩EQ=Q,∴面DEQ∥面ABF.而DE?面DEQ,
∴DE∥平面AFB.
(2)解:∵五边形ABCEF关于线段BC对称,
∴图(2)中延长DA、CB、EF,必交于一点G,
过点B作BH⊥DG于点H,连接HF.
又由五边形ABCEF关于线段BC对称知BF⊥BC,AB⊥BC,
而平面ABCD⊥平面ECBF,
∴FB⊥平面ECBF.∴∠BHF是二面角E-AD-B的平面角.
又∵FE⊥CE,∴AD⊥DC,∴△ABG∽△CDG,
∴
=
=
,解得AG=2,BG=
.
在RT△ABG中,BG•AB=AG•BH⇒BH=
.
∴RT△FBH中,FH=
=
,cos∠BHF=
=
,
∴二面角E-AD-B的余弦值为
.
向量法:
(1)证明:由五边形ABCEF关于线段BC对称知BF⊥BC,AB⊥BC,
而平面ABCD⊥平面ECBF,∴FB⊥平面ECBF,∴FB⊥AB.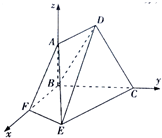
以B为坐标原点,建系如图.
则 A(0,0,1),F(1,0,0),D(0,
,
),E(
,
,0),
所以
=(1,0,-1),
=(
,0,-
),
∴
=
,∴AF∥DE,又AF?面ABF,DE?面ABF,
∴DE∥平面AFB.
(2)解:由(1)得A,D,F,E四点共面,
=(1,0,-1),
=(0,
,
),
设平面ADEF的一个法向量为
=(x,y,z),
则
,不妨令y=-1,则
=(
,-1,
),
又面ABCD的一个法向量是
=(1,0,0), ∴cos<
,
>=
.
∴二面角E-AD-B的余弦值为
.
(1)证明:如图,作DQ∥AB交BC于点Q,连接EQ.

∵五边形ABCEF关于线段BC对称,
∴EQ∥FB.
又DQ?面ABF,AB?面ABF,
∴DQ∥面AFB.同理:EQ∥面AFB.
又DQ∩EQ=Q,∴面DEQ∥面ABF.而DE?面DEQ,
∴DE∥平面AFB.
(2)解:∵五边形ABCEF关于线段BC对称,
∴图(2)中延长DA、CB、EF,必交于一点G,
过点B作BH⊥DG于点H,连接HF.
又由五边形ABCEF关于线段BC对称知BF⊥BC,AB⊥BC,
而平面ABCD⊥平面ECBF,
∴FB⊥平面ECBF.∴∠BHF是二面角E-AD-B的平面角.
又∵FE⊥CE,∴AD⊥DC,∴△ABG∽△CDG,
∴
| AG |
| GC |
| AB |
| CD |
| BG |
| DG |
| 3 |
在RT△ABG中,BG•AB=AG•BH⇒BH=
| ||
| 2 |
∴RT△FBH中,FH=
(
|
| ||
| 2 |
| BH |
| HF |
| ||
| 7 |
∴二面角E-AD-B的余弦值为
| ||
| 7 |
向量法:
(1)证明:由五边形ABCEF关于线段BC对称知BF⊥BC,AB⊥BC,
而平面ABCD⊥平面ECBF,∴FB⊥平面ECBF,∴FB⊥AB.

以B为坐标原点,建系如图.
则 A(0,0,1),F(1,0,0),D(0,
| ||
| 2 |
| 3 |
| 2 |
| 3 |
| 2 |
| ||
| 2 |
所以
| AF |
| DE |
| 3 |
| 2 |
| 3 |
| 2 |
∴
| AF |
| 3 |
| 2 |
| DE |
∴DE∥平面AFB.
(2)解:由(1)得A,D,F,E四点共面,
| AF |
| AD |
| ||
| 2 |
| 1 |
| 2 |
设平面ADEF的一个法向量为
| n |
则
|
| n |
| 3 |
| 3 |
又面ABCD的一个法向量是
| m |
| n |
| m |
| ||
| 7 |
∴二面角E-AD-B的余弦值为
| ||
| 7 |
点评:本题考查直线与平面平行的证明,考查二面角的余弦值的求法,解题时要认真审题,注意向量法的合理运用.

练习册系列答案
相关题目
设等差数列{an}的前n项和Sn,若S15>0,S16<0,则数列{
}的前15项中最大的项是( )
| Sn |
| an |
| A、第1项 | B、第8项 |
| C、第9项 | D、第15项 |
下列说法正确的是( )
| A、函数的极大值就是函数的最大值 |
| B、函数的极小值就是函数的最小值 |
| C、函数的最值一定是极值 |
| D、在闭区间上的连续函数一定存在最值 |
在△ABC中,若a=7,b=8,cosC=
,则c=( )
| 13 |
| 14 |
| A、1 | B、2 | C、3 | D、4 |
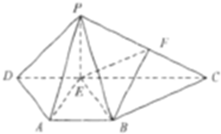 如图,在四棱维P-ABCD中,侧面PCD⊥底面ABCD.四边形ABCD是等腰梯形.AB∥CD.∠ADC=∠PDC=
如图,在四棱维P-ABCD中,侧面PCD⊥底面ABCD.四边形ABCD是等腰梯形.AB∥CD.∠ADC=∠PDC=