题目内容
3.我国古代数学典籍《九章算术》第七章“盈不足”中有一道两鼠穿墙问题:“今有垣厚五尺,两鼠对穿,大鼠日一尺,小鼠日一尺,大鼠日自倍,小鼠日自半,问何日相逢,各穿几何”,翻译过来就是:有五尺厚的墙,两只老鼠从墙的两边相对分别打洞穿墙,大、小鼠第一天都进一尺,以后每天,大鼠加倍,小鼠减半,则几天后两鼠相遇,这个问题体现了古代对数列问题的研究,现将墙的厚度改为1000尺,则需要几天时间才能打穿(结果取整数)( )| A. | 8 | B. | 9 | C. | 10 | D. | 11 |
分析 设需要n天时间才能打穿$\frac{{2}^{n}-1}{2-1}$+$\frac{1-\frac{1}{{2}^{n}}}{1-\frac{1}{2}}$≥1000,化为:2n-$\frac{2}{{2}^{n}}$-999≥0,令f(n)=2n-$\frac{2}{{2}^{n}}$-999,利用函数零点存在定理与函数的单调性即可得出
解答 解:设需要n天时间才能打穿,则$\frac{{2}^{n}-1}{2-1}$+$\frac{1-\frac{1}{{2}^{n}}}{1-\frac{1}{2}}$≥1000,
化为:2n-$\frac{2}{{2}^{n}}$-999≥0,
令f(n)=2n-$\frac{2}{{2}^{n}}$-999,则f(10)=1024-$\frac{1}{512}$-999>0.
f(9)=512-$\frac{1}{256}$-999<0.
f(x)=${2}^{x}-\frac{2}{{2}^{x}}$-999,(x≥1).
∴f(x)在(9,10)内存在一个零点.
又函数f(x)在x≥1时单调递增,因此f(x)在(9,10)内存在唯一一个零点.
∴需要10天时间才能打穿.
故选:C.
点评 本题考查了函数零点存在定理与函数的单调性、等比数列的通项公式与求和公式,考查了推理能力与计算能力,属于中档题.

练习册系列答案
 阳光课堂课时作业系列答案
阳光课堂课时作业系列答案
相关题目
14.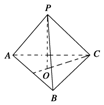 已知点P是正三角形ABC所在平面外一点,PA=PB=PC=$\frac{2}{3}$,AB=1,则PC和平面ABC所成的角是( )
已知点P是正三角形ABC所在平面外一点,PA=PB=PC=$\frac{2}{3}$,AB=1,则PC和平面ABC所成的角是( )
 已知点P是正三角形ABC所在平面外一点,PA=PB=PC=$\frac{2}{3}$,AB=1,则PC和平面ABC所成的角是( )
已知点P是正三角形ABC所在平面外一点,PA=PB=PC=$\frac{2}{3}$,AB=1,则PC和平面ABC所成的角是( )| A. | 90° | B. | 60° | C. | 45° | D. | 30° |
11.著名数学家华罗庚曾说过:“数形结合百般好,隔裂分家万事休.”事实上,有很多代数问题可以转化为几何问题加以解决,如:$\sqrt{(x-a)^{2}+(y-b)^{2}}$可以转化为平面上点M(x,y)与点N(a,b)的距离.结合上述观点,可得f(x)=$\sqrt{{x}^{2}+4x+20}$+$\sqrt{{x}^{2}+2x+10}$的最小值为( )
| A. | $3\sqrt{2}$ | B. | $4\sqrt{2}$ | C. | $5\sqrt{2}$ | D. | $7\sqrt{2}$ |
18.已知x>0,y>0且2x+3y=8,则$\frac{2}{x}+\frac{3}{y}$的最小值为( )
| A. | $\frac{25}{8}$ | B. | $\frac{25}{4}$ | C. | 25 | D. | $\frac{4}{25}$ |
8.为了得到函数y=sin(3x-$\frac{π}{3}$)的图象,只需要把函数y=sin3x的图象上所有点( )
| A. | 向左平行移动$\frac{π}{3}$个单位长度 | B. | 向右平行移动$\frac{π}{3}$个单位长 | ||
| C. | 向左平行移动$\frac{π}{9}$个单位长度 | D. | 向右平行移动$\frac{π}{9}$个单位长度 |
15.下列叙述中,正确的是( )
| A. | $\overrightarrow{AB}$+$\overrightarrow{BA}$=$\overrightarrow{0}$ | |
| B. | 若|$\overrightarrow{a}$|=|$\overrightarrow{b}$|且$\overrightarrow{a}$∥$\overrightarrow{b}$,则$\overrightarrow{a}$=$\overrightarrow{b}$ | |
| C. | 若|$\overrightarrow{a}$-$\overrightarrow{b}$|=|$\overrightarrow{a}$+$\overrightarrow{b}$|,则$\overrightarrow{a}$⊥$\overrightarrow{b}$ | |
| D. | 若向量$\overrightarrow{b}$与向量$\overrightarrow{a}$共线,则有且只有一个实数λ,使得$\overrightarrow{b}$=λ$\overrightarrow{a}$ |