题目内容
13.函数y=loga(x-2)+3(a>0,a≠1)的图象恒过一定点(3,3).分析 根据对数函数图象的性质,由对数函数恒过定点(1,0),再根据函数平移变换的公式,结合平移向量公式即可得到到正确结论.
解答 解:由函数图象的平移公式,我们可得:
将函数y=logax(a>0,a≠1)的图象向右平移2个单位,再向上平移3个单位
即可得到函数y=loga(x-2)+3(a>0,a≠1)的图象.
又∵函数y=logax(a>0,a≠1)的图象恒过(1,0)点,
由平移向量公式,易得函数y=loga(x-2)+3(a>0,a≠1)的图象恒过(3,3)点
故答案为:(3,3)
点评 本题考查的对数函数图象的性质,由对数函数恒过定点(1,0),再根据函数平移变换的公式,函数y=loga(x+m)+n(a>0,a≠1)的图象恒过(1-m,n)点.

练习册系列答案
 快乐暑假暑假能力自测中西书局系列答案
快乐暑假暑假能力自测中西书局系列答案
相关题目
5.底面为正方形的四棱锥,其一条测棱垂直于底面,则该四棱锥的三视图可以是下列各图中的( )
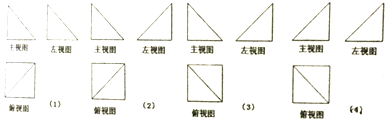

| A. | (1)(3) | B. | (1)(4) | C. | (2)(3) | D. | (2)(4) |