题目内容
设集合M={f(x)|x∈(0,+∞),f(x)=f(
)}.
(1)已知函数f(x)=
(x>0),求证:f(x)∈M;
(2)对于(1)中的函数f(x),求证:存在定义域为[2,+∞)的函数g(x),使得g(x+
)=f(x)对任意x>0成立.
(3)对于任意f(x)∈M,求证:存在定义域为[2,+∞)的函数g(x),使得等式g(x+
)=f(x)对任意x>0成立.
| 1 |
| x |
(1)已知函数f(x)=
| x |
| 1+x2 |
(2)对于(1)中的函数f(x),求证:存在定义域为[2,+∞)的函数g(x),使得g(x+
| 1 |
| x |
(3)对于任意f(x)∈M,求证:存在定义域为[2,+∞)的函数g(x),使得等式g(x+
| 1 |
| x |
考点:抽象函数及其应用,函数解析式的求解及常用方法
专题:函数的性质及应用
分析:(1)验证函数的表达式是否满足f(x)=f(
).从而得到结论.
(2)利用函数f(x)的解析式,求出g(x+
)的表达式,然后判断即可.
(3)通过函数的零点,讨论当x>0时,则g(x+
),当0<x<1时,g(x+
)当x>1时,g(x+
)的表达式是否满足题意即可.
| 1 |
| x |
(2)利用函数f(x)的解析式,求出g(x+
| 1 |
| x |
(3)通过函数的零点,讨论当x>0时,则g(x+
| 1 |
| x |
| 1 |
| x |
| 1 |
| x |
解答:
证明:(1)由f(x)=
(x>0)可得,f(
)=
=
,…3分
因此f(x)=f(
).又x>0,∴f(x)∈M.…4分
(2)由f(x)=
=
,
设函数g(x)=
(x≥2),当x>0时,x+
≥2
=2.…8分
则g(x+
)=
=
=f(x).…10分
即存在定义域为[2,+∞)的函数g(x),使得等式g(x+
)=f(x)对任意x>0成立.
(3)当x>0时,设x+
=t,则t≥2,
可得x2-tx+1=0,解得x=
,…12分
设函数g(x)=f(
)(x≥2),当x>0时,x+
≥2
=2.…13分
则g(x+
)=f(
)=f(
).…14分
当0<x<1时,x≤
,g(x+
)=f(
)=f(
)=f(x)…16分
当x>1时,x>
,g(x+
)=f(
)=f(x).…18分
即存在定义域为[2,+∞)的函数g(x),使得等式g(x+
)=f(x)对任意x>0成立.
| x |
| 1+x2 |
| 1 |
| x |
| ||
1+
|
| x |
| 1+x2 |
因此f(x)=f(
| 1 |
| x |
(2)由f(x)=
| x |
| 1+x2 |
| 1 | ||
x+
|
设函数g(x)=
| 1 |
| x |
| 1 |
| x |
x•
|
则g(x+
| 1 |
| x |
| 1 | ||
x+
|
| x |
| 1+x2 |
即存在定义域为[2,+∞)的函数g(x),使得等式g(x+
| 1 |
| x |
(3)当x>0时,设x+
| 1 |
| x |
可得x2-tx+1=0,解得x=
t±
| ||
| 2 |
设函数g(x)=f(
t+
| ||
| 2 |
| 1 |
| x |
x•
|
则g(x+
| 1 |
| x |
x+
| ||||||
| 2 |
x+
| ||||
| 2 |
当0<x<1时,x≤
| 1 |
| x |
| 1 |
| x |
x+
| ||||
| 2 |
| 1 |
| x |
当x>1时,x>
| 1 |
| x |
| 1 |
| x |
x+
| ||||
| 2 |
即存在定义域为[2,+∞)的函数g(x),使得等式g(x+
| 1 |
| x |
点评:本题考查函数性质的综合运用,考查学生对探究性理解水平,考查分析问题解决问题的能力.

练习册系列答案
相关题目
对于实数a和b,定义运算a*b,运算原理如图所示,则式子(
)-2*lne2的值为( )
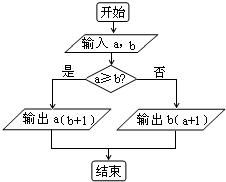
| 1 |
| 2 |

| A、8 | ||
| B、10 | ||
| C、12 | ||
D、
|
下列函数中周期为π且图象关于直线x=
对称的函数是( )
| π |
| 3 |
A、y=2sin(
| ||||
B、y=2sin(2x-
| ||||
C、y=2sin(2x+
| ||||
D、y=2sin(
|