��Ŀ����
��֪��ԲM��
+
=1(a��b��0)��������e=
�����߷���Ϊx=-4��
��1������ԲM�ı����̣�
��2����֪����Բ
+
=1��һ�㣨x0��y0������Բ�����ߣ����߷���Ϊ
+
=1���ֹ���ԲM���ҽ�����б�ʲ�Ϊ0��ֱ��l����Բ����A��B���㣬��A��B�ֱ�����Բ������l1��l2��
��֤����l1��l2�Ľ���P��һ����ֱ���ϣ�
�����ABP�������Сֵ��
| x2 |
| a2 |
| y2 |
| b2 |
| 1 |
| 2 |
��1������ԲM�ı����̣�
��2����֪����Բ
| x2 |
| a2 |
| y2 |
| b2 |
| x0x |
| a2 |
| y0y |
| b2 |
��֤����l1��l2�Ľ���P��һ����ֱ���ϣ�
�����ABP�������Сֵ��
���㣺ֱ����Բ���ߵ��ۺ�����
ר�⣺�ۺ���,Բ���ߵĶ��塢�����뷽��
��������1��������ԲM��
+
=1(a��b��0)��������e=
�����߷���Ϊx=-4�����������飬��������������������ԲM�ı����̣�
��2������ֱ��AB��x=my+1��A��x1��y1����B��x2��y2�����������߷���Ϊ
+
=1��
+
=1���ɵý���P�������꣬�������P�ĺ����꣬���ɵó����ۣ�
��ֱ��AB��x=my+1������
+
=1������Τ�ﶨ��������ҳ�|AB|�����P��4��-3m����ֱ��AB�ľ��룬�ɵá�ABP�������Ԫ�����������ABP�������Сֵ��
| x2 |
| a2 |
| y2 |
| b2 |
| 1 |
| 2 |
��2������ֱ��AB��x=my+1��A��x1��y1����B��x2��y2�����������߷���Ϊ
| x1x |
| 4 |
| y1y |
| 3 |
| x2x |
| 4 |
| y2y |
| 3 |
��ֱ��AB��x=my+1������
| x2 |
| 4 |
| y2 |
| 3 |
���
��1���⣺����ԲM��
+
=1(a��b��0)��������e=
�����߷���Ϊx=-4��
��
����a=2��c=1��
��b=
=
��
����ԲM�ı�����Ϊ
+
=1��
��2����֤������ֱ��AB��x=my+1��A��x1��y1����B��x2��y2����
�������߷���Ϊ
+
=1��
+
=1��
�ɵý���P��������Ϊy=
=
=-3m��
��ʽ����ɵ�
+
=0��
y=-3m���룬�ɵ�x=-4��
��l1��l2�Ľ���P��һ����ֱ��x=-4�ϣ�
�ڽ⣺P��4��-3m����ֱ��AB�ľ���d=
��
ֱ��AB��x=my+1������
+
=1���ɵã�3m2+4��y2+6my-9=0��
��y1+y2=-
��y1y2=
��
��|AB|=
•|y1-y2|=
���ABP���ΪS=
|AB|d=
��
��t=
��1����S=
=
��
��u=
�ʣ�0��1]����S=
����u�ʣ�0��1]�ϵ����ݼ���
�൱u=1����t=1����m=0ʱ����ABP�������СֵΪ
��
| x2 |
| a2 |
| y2 |
| b2 |
| 1 |
| 2 |
��
|
��b=
| a2-c2 |
| 3 |
����ԲM�ı�����Ϊ
| x2 |
| 4 |
| y2 |
| 3 |
��2����֤������ֱ��AB��x=my+1��A��x1��y1����B��x2��y2����
�������߷���Ϊ
| x1x |
| 4 |
| y1y |
| 3 |
| x2x |
| 4 |
| y2y |
| 3 |
�ɵý���P��������Ϊy=
| 3(x2-x1) |
| x2y1-x1y2 |
| 3(my2-my1) |
| (my2+1)y1-(my1+1)y2 |
��ʽ����ɵ�
| mx |
| 4 |
| y |
| 3 |
y=-3m���룬�ɵ�x=-4��
��l1��l2�Ľ���P��һ����ֱ��x=-4�ϣ�
�ڽ⣺P��4��-3m����ֱ��AB�ľ���d=
| |-3m2-4+1| | ||
|
ֱ��AB��x=my+1������
| x2 |
| 4 |
| y2 |
| 3 |
��y1+y2=-
| 6m |
| 3m2+4 |
| 9 |
| 3m2+4 |
��|AB|=
| 1+m2 |
| 12(m2+1) |
| 3m2+4 |
���ABP���ΪS=
| 1 |
| 2 |
18(
| ||
| 3(m2+1)+1 |
��t=
| m2+1 |
| 18t3 |
| 3t2+1 |
| 18 | ||||
|
��u=
| 1 |
| t |
| 18 |
| 3u+u3 |
�൱u=1����t=1����m=0ʱ����ABP�������СֵΪ
| 9 |
| 2 |
���������⿼����Բ�ķ��������ʣ�������Բ�����߷��̣�����ֱ������Բ��λ�ù�ϵ����������������ļ��㣬�Ѷȴ�

��ϰ��ϵ�д�
 ���ɶ��ȫ���ƿؾ�ϵ�д�
���ɶ��ȫ���ƿؾ�ϵ�д�
�����Ŀ
�ڡ�ABC�У���AB=2��AC=3����A=60�㣬��BC�ij�Ϊ��������
A��
| ||
B��
| ||
| C��3 | ||
D��
|
��֪
��
��ƽ����������λ���������ǵļн�Ϊ60�㣬��2
-
��
�ļн��ǣ�������
| AB |
| AC |
| AB |
| AC |
| CA |
| A��30�� | B��60�� |
| C��90�� | D��120�� |

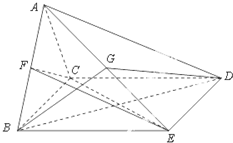 ��ͼ������A-BCDE�У���ABC���������Σ��ı���BCDE�Ǿ��Σ���ƽ��ABC��ƽ��BCDE��AB=2��AD=4��
��ͼ������A-BCDE�У���ABC���������Σ��ı���BCDE�Ǿ��Σ���ƽ��ABC��ƽ��BCDE��AB=2��AD=4�� ��ͼ��������ABC-A1B1C1�IJ���AA1��ƽ��ABC����ABCΪ�������Σ�����AA1C1C�������Σ�E��A1B���е㣬F����CC1�ϵĵ㣮
��ͼ��������ABC-A1B1C1�IJ���AA1��ƽ��ABC����ABCΪ�������Σ�����AA1C1C�������Σ�E��A1B���е㣬F����CC1�ϵĵ㣮