题目内容
已知Rt△ABC的斜边为10,内切圆的半径为2,则两条直角边的长为( )
A、5和5
| ||||
B、4
| ||||
| C、6和8 | ||||
| D、5和7 |
考点:圆內接多边形的性质与判定
专题:立体几何
分析:根据直角三角形内切圆半径公式及勾股定理构造方程组,解方程组可得答案.
解答:
解:设Rt△ABC的两条直角边长为a,b,
则∵Rt△ABC的斜边为10,内切圆的半径为2,
a+b-10=2×2,
a2+b2=102,
解得:a=6,b=8,或a=8,b=6,
故选:C
则∵Rt△ABC的斜边为10,内切圆的半径为2,
a+b-10=2×2,
a2+b2=102,
解得:a=6,b=8,或a=8,b=6,
故选:C
点评:本题考查的知识点是直角三角形内切圆半径公式及勾股定理,难度不大,属于基础题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
已知△ABC的三边长BC=a,AC=b,AB=c,O为△ABC所在平面内一点,若a
+b
+c
=
,则点O是△ABC的( )
| OA |
| OB |
| OC |
| 0 |
| A、外心 | B、内心 | C、重心 | D、垂心 |
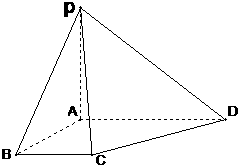 如图,在四棱锥P-ABCD中,底面ABCD为直角梯形,∠BAD=90°,BC∥AD,PA⊥底面ABCD,BC=AB=1,PA=AD=2
如图,在四棱锥P-ABCD中,底面ABCD为直角梯形,∠BAD=90°,BC∥AD,PA⊥底面ABCD,BC=AB=1,PA=AD=2