题目内容
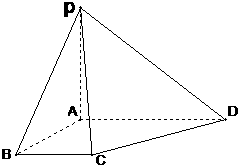 如图,在四棱锥P-ABCD中,底面ABCD为直角梯形,∠BAD=90°,BC∥AD,PA⊥底面ABCD,BC=AB=1,PA=AD=2
如图,在四棱锥P-ABCD中,底面ABCD为直角梯形,∠BAD=90°,BC∥AD,PA⊥底面ABCD,BC=AB=1,PA=AD=2(1)证明:AB⊥PD;
(2)求直线AB与直线PC夹角的余弦值.
考点:异面直线及其所成的角,空间中直线与直线之间的位置关系
专题:计算题,作图题,空间位置关系与距离
分析:(1)由题意可证PA⊥AB,结合BA⊥AD可得AB⊥平面PAD,从而得证;
(2)取AD的中点E,连结CE,PE;可知∠PCE为直线AB与直线PC的夹角,在Rt△PCE中解角的余弦值.
(2)取AD的中点E,连结CE,PE;可知∠PCE为直线AB与直线PC的夹角,在Rt△PCE中解角的余弦值.
解答:
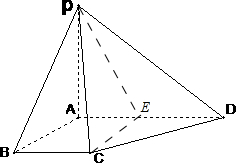 解:(1)证明:∵PA⊥底面ABCD,
解:(1)证明:∵PA⊥底面ABCD,
∴PA⊥AB,
又∵∠BAD=90°,
∴BA⊥AD,
∴AB⊥平面PAD,
∴AB⊥PD;
(2)取AD的中点E,连结CE,PE;
∵AE=BC=1,AB∥BC,
∴ABCE是平行四边形,
∴AB∥CE,
∴∠PCE为直线AB与直线PC的夹角,
又∵AB⊥平面PAD,
∴CE⊥平面PAD,
∴△PCE为直角三角形,
其中PC=
=
,
CE=1,
故cos∠PCE=
=
.
 解:(1)证明:∵PA⊥底面ABCD,
解:(1)证明:∵PA⊥底面ABCD,∴PA⊥AB,
又∵∠BAD=90°,
∴BA⊥AD,
∴AB⊥平面PAD,
∴AB⊥PD;
(2)取AD的中点E,连结CE,PE;
∵AE=BC=1,AB∥BC,
∴ABCE是平行四边形,
∴AB∥CE,
∴∠PCE为直线AB与直线PC的夹角,
又∵AB⊥平面PAD,
∴CE⊥平面PAD,
∴△PCE为直角三角形,
其中PC=
| 1+1+4 |
| 6 |
CE=1,
故cos∠PCE=
| 1 | ||
|
| ||
| 6 |
点评:本题考查了空间中垂直的判断与证明,同时考查了异面直线的角的解法,属于中档题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
函数y=sin2x+2
sin2x的最小正周期T为( )
| 3 |
| A、π | ||
| B、2π | ||
C、
| ||
D、
|
已知函数y=f(x)(x∈R)满足f(x+2)=f(x),且x∈[-1,1]时,f(x)=-|x|+1,则当x∈(0,6]时,函数g(x)=f(x)-log3x的零点个数为( )
| A、5 | B、6 | C、7 | D、8 |
已知Rt△ABC的斜边为10,内切圆的半径为2,则两条直角边的长为( )
A、5和5
| ||||
B、4
| ||||
| C、6和8 | ||||
| D、5和7 |
 如图所示,平面四边形EFGH的四个顶点分别在空间四边形ABCD的四边上,且直线EH与FG相交于点P,求证:B、D、P三点共线.
如图所示,平面四边形EFGH的四个顶点分别在空间四边形ABCD的四边上,且直线EH与FG相交于点P,求证:B、D、P三点共线. 如图1,在直角梯形ABCD中,AD∥BC,AB=2,BC=4,∠ABC=60°,沿对角线AC将梯形折成几何体PACD,并使得∠PAD=90°(如图2所示).
如图1,在直角梯形ABCD中,AD∥BC,AB=2,BC=4,∠ABC=60°,沿对角线AC将梯形折成几何体PACD,并使得∠PAD=90°(如图2所示).