题目内容
为了解某班学生喜爱打篮球是否与性别有关,对本班60人进行了问卷调查得到了如下的2×2列联表:
(I)用分层抽样的方法在喜爱打篮球的学生中抽6人,其中男生抽多少人?
(Ⅱ)在上述抽取的人中选2人,求恰有一名女生的概率;
(Ⅲ)你是否有95%的把握认为喜爱打篮球与性别有关?说明你的理由.
下面的临界值表供参考:
(参考公式:X2=
,其中n=n11+n12+n21+n12或K2=
其中n=a+b+c+d))
| 喜爱打篮球 | 不喜爱打篮球 | 合计 | |
| 男生 | 24 | 8 | 32 |
| 女生 | 12 | 16 | 28 |
| 合计 | 36 | 24 | 60 |
(Ⅱ)在上述抽取的人中选2人,求恰有一名女生的概率;
(Ⅲ)你是否有95%的把握认为喜爱打篮球与性别有关?说明你的理由.
下面的临界值表供参考:
| P(X2≥x0)或P(K2≥k0) | 0.10 | 0.05 | 0.010 | 0.005 |
| x0(或k0) | 2.706 | 3.841 | 6.635 | 7.879 |
| n(n11n13-n13n21)2 |
| n1+n2+n+1n+1 |
| n(nd-bc)2 |
| (a+b)(c+d)(a+c)(b+d) |
考点:独立性检验
专题:概率与统计
分析:(I)根据分层抽样方法的特点,计算抽取比例是多少,由此求出男生应抽取的人数;
(Ⅱ)计算在上述抽取的6人中,女生、男生是多少,利用列举法求出基本事件数,求出对应的概率;
(Ⅲ)计算x2的值,通过表中数据,作出判断.
(Ⅱ)计算在上述抽取的6人中,女生、男生是多少,利用列举法求出基本事件数,求出对应的概率;
(Ⅲ)计算x2的值,通过表中数据,作出判断.
解答:
解:(I)在喜爱打篮球的学生中抽6人,则抽取比例为
=
,
∴男生应抽取24×
=4人;
(Ⅱ)在上述抽取的6人中,女生2人,男生4人,
女生记为A、B,男生记为c、d、e、f;
从6人中选2人,基本事件为
AB、Ac、Ad、Ae、Af、Bc、Bd、Be、Bf、cd、ce、cf、de、df、ef共15种,
其中恰有一名女生的情况为AB、Ac、Ad、Ae、Af、Bc、Bd、Be、Bf共8种,
∴抽取的6名女生中,恰有1名女生的概率为P=
;
(Ⅲ)∵x2=
≈6.429,
6.429>3.841,
∴有95%的把握认为喜爱打篮球与性别有关.
| 6 |
| 36 |
| 1 |
| 6 |
∴男生应抽取24×
| 1 |
| 6 |
(Ⅱ)在上述抽取的6人中,女生2人,男生4人,
女生记为A、B,男生记为c、d、e、f;
从6人中选2人,基本事件为
AB、Ac、Ad、Ae、Af、Bc、Bd、Be、Bf、cd、ce、cf、de、df、ef共15种,
其中恰有一名女生的情况为AB、Ac、Ad、Ae、Af、Bc、Bd、Be、Bf共8种,
∴抽取的6名女生中,恰有1名女生的概率为P=
| 8 |
| 15 |
(Ⅲ)∵x2=
| 60×(24×16-12×8)2 |
| 36×24×32×28 |
| 45 |
| 7 |
6.429>3.841,
∴有95%的把握认为喜爱打篮球与性别有关.
点评:本题考查了分层抽样方法的应用问题,也考查了用列举法求求古典概型的概率问题,利用二联表估计数据的特征等问题,是综合性题目.

练习册系列答案
 每课必练系列答案
每课必练系列答案
相关题目
函数f(x)=4x-x4的图象大致是( )
A、 |
B、 |
C、 |
D、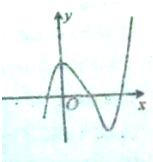 |
已知函数f(x)=
,若不等式f(x)<0的解集为非空集合D,且D⊆(-1,2),则z=2a-b的取值范围为( )
|
| A、(4,+∞) |
| B、[-4,+∞) |
| C、(-∞,4) |
| D、(-1,4) |
已知正项等比数列{an}中,3a1,
a3,2a2成等差数列,则
=( )
| 1 |
| 2 |
| a2011+a2012 |
| a2009+a2010 |
| A、3或-1 | B、9或1 | C、1 | D、9 |
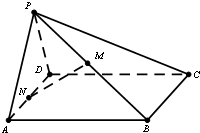 如图,边长为4的正方形ABCD与正三角形ADP所在的平面相互垂直,且M、N分别为PB、AD中点.
如图,边长为4的正方形ABCD与正三角形ADP所在的平面相互垂直,且M、N分别为PB、AD中点.