题目内容
已知点P(1,1)是函数f(x)=lnx+
ax2-(a+1)x的图象上一点.
(1)求f(x)的单调区间.
(2)证明:存在a∈(1,+∞),使得f(a)=f(
);
(3)记函数y=f(x)的图象为曲线C,设点A(x1,y1),B(x2,y2)是曲线C上的不同两点,如果在曲线C上存在点M(x0,y0),使得①:x0=
;②:曲线C在点M处的切线平行于直线AB,则称函数f(x)存在“中值相依切线”,试问:函数f(x)是否存在“中值相依切线”,请说明理由.
| 1 |
| 2 |
(1)求f(x)的单调区间.
(2)证明:存在a∈(1,+∞),使得f(a)=f(
| 1 |
| 3 |
(3)记函数y=f(x)的图象为曲线C,设点A(x1,y1),B(x2,y2)是曲线C上的不同两点,如果在曲线C上存在点M(x0,y0),使得①:x0=
| x1+x2 |
| 2 |
考点:利用导数研究曲线上某点切线方程,利用导数研究函数的单调性
专题:计算题,证明题,压轴题,导数的综合应用
分析:(1)先求函数f(x)的定义域,代入点P(1,1)求a,从而化简函数并确定函数的单调性;
(2)设g(x)=f(x)-f(
),由于f(x)在(0,1)内单调递增知f(1)>f(
),从而得即g(1)>0;再取x′=2e>1,从而得g(x′)=e(
+6-8e)<0,从而证明;
(3)假设函数f(x)存在“中值相依切线”,设A(x1,y1),B(x2,y2)是曲线y=f(x)上的不同两点,且0<x1<x2,从而化简可得ln
=
=
;令
=t(t>1),化为lnt=
=2-
,lnt+
=2;再令h(t)=lnt+
,求导h′(t)=
-
=
;从而解得.
(2)设g(x)=f(x)-f(
| 1 |
| 3 |
| 1 |
| 3 |
ln6+
| ||
| e |
(3)假设函数f(x)存在“中值相依切线”,设A(x1,y1),B(x2,y2)是曲线y=f(x)上的不同两点,且0<x1<x2,从而化简可得ln
| x2 |
| x1 |
| 2(x2-x1) |
| x2+x1 |
2(
| ||
|
| x2 |
| x1 |
| 2(t-1) |
| t+1 |
| 4 |
| t+1 |
| 4 |
| t+1 |
| 4 |
| t+1 |
| 1 |
| t |
| 4 |
| (t+1)2 |
| (t-1)2 |
| t(t+1)2 |
解答:
解:(1)函数f(x)的定义域是(0,+∞).
∵点P(1,1)是函数f(x)=lnx+
ax2-(a+1)x的图象上一点,
∴
a-(a+1)=1,a=-4,
f(x)=lnx-2x2+3x.
∴f′(x)=
.
∴f(x) 在(0,1)上单调递增,在(1,+∞)上单调递减.
(2)证明:由(1)知f(x)在(0,1)内单调递增,在(1,+∞)内单调递减.
设g(x)=f(x)-f(
),由于f(x)在(0,1)内单调递增,
故f(1)>f(
) 即g(1)>0.
取x′=2e>1,则g(x′)=e(
+6-8e)<0,
所以存在α∈(1,x′),使f(α)=f(
).
即存在α∈(1,+∞),使f(α)=f(
).
(3)假设函数f(x)存在“中值相依切线”.
设A(x1,y1),B(x2,y2)是曲线y=f(x)上的不同两点,且0<x1<x2,
则y1=lnx1-2x12+3x1,y2=lnx2-2x22+3x2.
kAB=
=
=
-2(x1+x2)+3.
曲线在点M(x0,y0)处的切线斜率k=f′(x0)=f′(
)=
-2(x1+x2)+3;
依题意得:
-2(x1+x2)+3=
-2(x1+x2)+3;
化简可得:
=
,
即ln
=
=
.
设
=t(t>1),上式可化为lnt=
=2-
,lnt+
=2;
令h(t)=lnt+
,
h′(t)=
-
=
.
因为t>1,显然h′(t)>0,所以在(1,+∞)上递增,
显然有h(t)>2恒成立.所以在(1,+∞)内不存在,使得lnt+
=2成立.
综上所述,假设不成立.所以,函数f(x)不存在“中值相依切线”.
∵点P(1,1)是函数f(x)=lnx+
| 1 |
| 2 |
∴
| 1 |
| 2 |
f(x)=lnx-2x2+3x.
∴f′(x)=
| (x-1)(4x+1) |
| x |
| x | (0,1) | 1 | (1,+∞) |
| f′(x) | + | 0 | - |
| f(x) | ↗ | 1 | ↘ |
(2)证明:由(1)知f(x)在(0,1)内单调递增,在(1,+∞)内单调递减.
设g(x)=f(x)-f(
| 1 |
| 3 |
故f(1)>f(
| 1 |
| 3 |
取x′=2e>1,则g(x′)=e(
ln6+
| ||
| e |
所以存在α∈(1,x′),使f(α)=f(
| 1 |
| 3 |
即存在α∈(1,+∞),使f(α)=f(
| 1 |
| 3 |
(3)假设函数f(x)存在“中值相依切线”.
设A(x1,y1),B(x2,y2)是曲线y=f(x)上的不同两点,且0<x1<x2,
则y1=lnx1-2x12+3x1,y2=lnx2-2x22+3x2.
kAB=
| y2-y1 |
| x2-x1 |
lnx2-lnx1-2(
| ||||
| x2-x1 |
| lnx2-lnx1 |
| x2-x1 |
曲线在点M(x0,y0)处的切线斜率k=f′(x0)=f′(
| x1+x2 |
| 2 |
| 2 |
| x1+x2 |
依题意得:
| lnx2-lnx1 |
| x2-x1 |
| 2 |
| x1+x2 |
化简可得:
| lnx2-lnx1 |
| x2-x1 |
| 2 |
| x1+x2 |
即ln
| x2 |
| x1 |
| 2(x2-x1) |
| x2+x1 |
2(
| ||
|
设
| x2 |
| x1 |
| 2(t-1) |
| t+1 |
| 4 |
| t+1 |
| 4 |
| t+1 |
令h(t)=lnt+
| 4 |
| t+1 |
h′(t)=
| 1 |
| t |
| 4 |
| (t+1)2 |
| (t-1)2 |
| t(t+1)2 |
因为t>1,显然h′(t)>0,所以在(1,+∞)上递增,
显然有h(t)>2恒成立.所以在(1,+∞)内不存在,使得lnt+
| 4 |
| t+1 |
综上所述,假设不成立.所以,函数f(x)不存在“中值相依切线”.
点评:本题考查了导数的综合应用及学生的化简与构造函数的能力,属于难题.

练习册系列答案
 快捷英语周周练系列答案
快捷英语周周练系列答案
相关题目
双曲线2x2-y2=1的离心率为( )
A、
| ||||
B、
| ||||
C、
| ||||
D、
|
直线y=x-1与双曲线x2-
=1(b>0)有两个不同的交点,则此双曲线离心率的范围是( )
| y2 |
| b2 |
A、(1,
| ||||
B、(
| ||||
| C、(1,+∞) | ||||
D、(1,
|
已知平面α⊥平面β,交于直线l,且直线a?α,直线b?β,则下列命题错误的是( )
| A、若a∥b,则a∥l或b∥l |
| B、若a⊥b,则a⊥l且b⊥l |
| C、若直线a,b都不平行直线l,则直线a必不平行直线b |
| D、若直线a,b都不垂直直线l,则直线a必不垂直直线b |
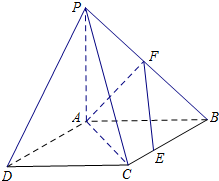 如图,四边形ABCD是正方形,△PAB与△PAD均是以A为直角顶点的等腰直角三角形,点F是PB的中点,点E是边BC上的任意一点.
如图,四边形ABCD是正方形,△PAB与△PAD均是以A为直角顶点的等腰直角三角形,点F是PB的中点,点E是边BC上的任意一点.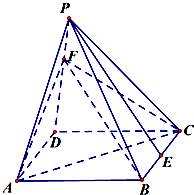 如图,在正四棱锥P-ABCD中,底面是边长为2的正方形,侧棱PA=
如图,在正四棱锥P-ABCD中,底面是边长为2的正方形,侧棱PA=