题目内容
若点M到x轴的距离是它到y轴距离的2倍,则点M的轨迹方程是 .
考点:轨迹方程
专题:计算题,直线与圆
分析:设M(x,y),利用点M到x轴的距离是它到y轴距离的2倍,可得|y|=2|x|,即可求出点M的轨迹方程.
解答:
解:设M(x,y),则
∵点M到x轴的距离是它到y轴距离的2倍,
∴|y|=2|x|,
∴y=±2x,
故答案为:y=±2x.
∵点M到x轴的距离是它到y轴距离的2倍,
∴|y|=2|x|,
∴y=±2x,
故答案为:y=±2x.
点评:本题考查点M的轨迹方程,考查学生的计算能力,比较基础.

练习册系列答案
 尖子生新课堂课时作业系列答案
尖子生新课堂课时作业系列答案
相关题目
定义域为R的奇函数f(x),当x∈(-∞,0)时f(x)+xf′(x)<0恒成立,若a=2f(2),b=ln2•f(ln2),c=-f(-1),则a,b,c的大小关系为( )
| A、a>b>c |
| B、c>b>a |
| C、a>c>b |
| D、b>c>a |
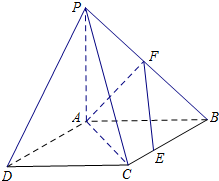 如图,四边形ABCD是正方形,△PAB与△PAD均是以A为直角顶点的等腰直角三角形,点F是PB的中点,点E是边BC上的任意一点.
如图,四边形ABCD是正方形,△PAB与△PAD均是以A为直角顶点的等腰直角三角形,点F是PB的中点,点E是边BC上的任意一点.