题目内容
已知双曲线
-
=1(a>0,b>0)的右焦点为F,过F的直线l交双曲线的渐近线于A,B两点,且与其中一条渐近线垂直,若
=4
,则该双曲线的离心率为 .
| x2 |
| a2 |
| y2 |
| b2 |
| AF |
| FB |
考点:双曲线的简单性质
专题:计算题,直线与圆,圆锥曲线的定义、性质与方程
分析:由题意得右焦点F(c,0),设一渐近线OA的方程为y=
x,则另一渐近线OB的方程为y=-
x,设A(m,
),B(n,-
),由
=4
,得到m,n的关系,求出A,B的坐标,由FB⊥OB可得,斜率之积等于-1,进而可得a、b的关系式,结合双曲线a、b、c的关系,可得离心率.
| b |
| a |
| b |
| a |
| bm |
| a |
| bn |
| a |
| AF |
| FB |
解答:
解:由题意得右焦点F(c,0),设一渐近线OA的方程为y=
x,
则另一渐近线OB的方程为y=-
x,
设A(m,
),B(n,-
),
∵
=4
,
∴(c-m,-
)=4(n-c,-
),
∴c-m=4(n-c),-
=-4
,解之可得m=
,n=
,
∴B(
,-
),由FB⊥OB可得,斜率之积等于-1,
即
•
=-1,化简可得5b2=3a2,即5(c2-a2)=3a2,
解之可得5c2=8a2,即e=
=
.
故答案为:
.
| b |
| a |
则另一渐近线OB的方程为y=-
| b |
| a |
设A(m,
| bm |
| a |
| bn |
| a |
∵
| AF |
| FB |
∴(c-m,-
| bm |
| a |
| bn |
| a |
∴c-m=4(n-c),-
| bm |
| a |
| bn |
| a |
| 5c |
| 2 |
| 5c |
| 8 |
∴B(
| 5c |
| 8 |
| 5bc |
| 8a |
即
| ||
|
| ||
|
解之可得5c2=8a2,即e=
| c |
| a |
2
| ||
| 5 |
故答案为:
2
| ||
| 5 |
点评:本题考查双曲线的简单性质,涉及离心率的求解,考查向量共线知识,属中档题.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
已知平面α⊥平面β,交于直线l,且直线a?α,直线b?β,则下列命题错误的是( )
| A、若a∥b,则a∥l或b∥l |
| B、若a⊥b,则a⊥l且b⊥l |
| C、若直线a,b都不平行直线l,则直线a必不平行直线b |
| D、若直线a,b都不垂直直线l,则直线a必不垂直直线b |
在集合{a,b,c,d}上定义两种运算⊕和?如下,那么d?(a⊕c)=( )


| A、a | B、b | C、c | D、d |
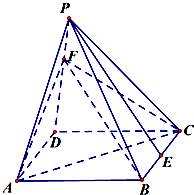 如图,在正四棱锥P-ABCD中,底面是边长为2的正方形,侧棱PA=
如图,在正四棱锥P-ABCD中,底面是边长为2的正方形,侧棱PA= 如图是某班第1和第2小组学生身高的茎叶图(单位:cm),则这两个小组学生身高中位数的等差中项为
如图是某班第1和第2小组学生身高的茎叶图(单位:cm),则这两个小组学生身高中位数的等差中项为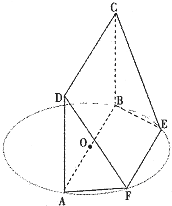 AB为圆O的直径,点E、F在圆上,AB∥EF,矩形ABCD所在平面与圆O所在平面互相垂直,已知AB=2,BC=EF=1.
AB为圆O的直径,点E、F在圆上,AB∥EF,矩形ABCD所在平面与圆O所在平面互相垂直,已知AB=2,BC=EF=1.