题目内容
已知正项等比数列{an}中,3a1,
a3,2a2成等差数列,则
=( )
| 1 |
| 2 |
| a2011+a2012 |
| a2009+a2010 |
| A、3或-1 | B、9或1 | C、1 | D、9 |
考点:等差数列与等比数列的综合
专题:等差数列与等比数列
分析:由已知得3a1+2a2=a3,从而q=3,由此求出
=
=32=9.
| a2011+a2012 |
| a2009+a2010 |
| a1•32010+a1•32011 |
| a1•32008+a1•32009 |
解答:
解:∵正项等比数列{an}中,3a1,
a3,2a2成等差数列,
∴3a1+2a2=a3,
∴3a1+2a1q=a1q2,
∴q2-2q-3=0,∵q>0,∴q=3,
∴
=
=32=9.
故选:D.
| 1 |
| 2 |
∴3a1+2a2=a3,
∴3a1+2a1q=a1q2,
∴q2-2q-3=0,∵q>0,∴q=3,
∴
| a2011+a2012 |
| a2009+a2010 |
| a1•32010+a1•32011 |
| a1•32008+a1•32009 |
故选:D.
点评:本题考查等比数列中两项之和的比值的求法,是中档题,解题时要注意等差数列和等比数列的性质的合理运用.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
已知平面α⊥平面β,交于直线l,且直线a?α,直线b?β,则下列命题错误的是( )
| A、若a∥b,则a∥l或b∥l |
| B、若a⊥b,则a⊥l且b⊥l |
| C、若直线a,b都不平行直线l,则直线a必不平行直线b |
| D、若直线a,b都不垂直直线l,则直线a必不垂直直线b |
 若程序框图如图所示,视x为自变量,y为函数值,可得函数y=f(x)的解析式,则f(x)>f(2)的解集为( )
若程序框图如图所示,视x为自变量,y为函数值,可得函数y=f(x)的解析式,则f(x)>f(2)的解集为( )| A、(2,+∞) |
| B、(4,5] |
| C、(-∞,-2]4 |
| D、(-∞,-2)∪(3,5,5] |
在集合{a,b,c,d}上定义两种运算⊕和?如下,那么d?(a⊕c)=( )


| A、a | B、b | C、c | D、d |
已知函数f(x)=
,则f[f(
)]=( )
|
| 1 |
| 8 |
| A、9 | ||
B、
| ||
C、
| ||
| D、27 |
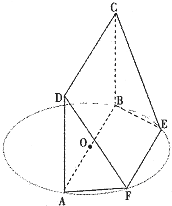 AB为圆O的直径,点E、F在圆上,AB∥EF,矩形ABCD所在平面与圆O所在平面互相垂直,已知AB=2,BC=EF=1.
AB为圆O的直径,点E、F在圆上,AB∥EF,矩形ABCD所在平面与圆O所在平面互相垂直,已知AB=2,BC=EF=1.