题目内容
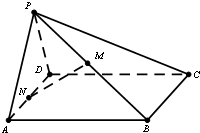 如图,边长为4的正方形ABCD与正三角形ADP所在的平面相互垂直,且M、N分别为PB、AD中点.
如图,边长为4的正方形ABCD与正三角形ADP所在的平面相互垂直,且M、N分别为PB、AD中点.(1)求证:MN∥面PCD;
(2)求直线PC与平面PNB所成角的正弦值.
考点:直线与平面所成的角,直线与平面平行的判定
专题:空间位置关系与距离,空间角
分析:(1)取PC的中点G,连结MG、DG,由已知得四边形DNMG为平行四边形,由此能证明MN∥面PDC.
(2)连接BN、NC、PN,过点C作CH⊥BN,垂足为H,连结PH由已知得∠CPH为直线PC与平面PNB所成的角,由此能求出直线PC与平面PNB所成角的正弦值.
(2)连接BN、NC、PN,过点C作CH⊥BN,垂足为H,连结PH由已知得∠CPH为直线PC与平面PNB所成的角,由此能求出直线PC与平面PNB所成角的正弦值.
解答:
(1)证明:取PC的中点G,连结MG、DG,在△PBC中,
∵M、G分别为PB、PC的中点,∴MG∥BC,且MG=
BC,又ND=
AD,
∴MG
DN,故四边形DNMG为平行四边形,
∴MN∥DG,又DG?平面PDC,M?N平面PDC,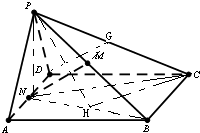
∴MN∥面PDC.…(6分)
(2)解:连接BN、NC、PN,因为面ADP⊥面ABCD,且PN⊥AD,
所以PN⊥面ABCD,又PN?面PNB,所以面PNB⊥面ABCD.
过点C作CH⊥BN,垂足为H,连结PH,∴CH⊥面PNB,
故∠CPH为直线PC与平面PNB所成的角,…(8分)
在正方形ABCD中,由已知条件,令∠ABN=∠BCH=θ,
∴CH=BCcosθ=4×
=
,…(10分)
在Rt△PNC中,∵PN=2
,NC=2
,∴PC=4
,
在Rt△CHP中,sin∠CPH=
=
=
.…(12分)
∵M、G分别为PB、PC的中点,∴MG∥BC,且MG=
| 1 |
| 2 |
| 1 |
| 2 |
∴MG
| ∥ |
. |
∴MN∥DG,又DG?平面PDC,M?N平面PDC,

∴MN∥面PDC.…(6分)
(2)解:连接BN、NC、PN,因为面ADP⊥面ABCD,且PN⊥AD,
所以PN⊥面ABCD,又PN?面PNB,所以面PNB⊥面ABCD.
过点C作CH⊥BN,垂足为H,连结PH,∴CH⊥面PNB,
故∠CPH为直线PC与平面PNB所成的角,…(8分)
在正方形ABCD中,由已知条件,令∠ABN=∠BCH=θ,
∴CH=BCcosθ=4×
| 2 | ||
|
| 8 | ||
|
在Rt△PNC中,∵PN=2
| 3 |
| 5 |
| 2 |
在Rt△CHP中,sin∠CPH=
| CH |
| PC |
| 8 | ||||
4
|
| ||
| 5 |
点评:本题考查空间线面关系、几何体的体积等知识,考查数形结合、化归与转化的数学思想方法,以及空间想象能力、推理论证能力和运算求解能力.

练习册系列答案
相关题目
定义域为R的奇函数f(x),当x∈(-∞,0)时f(x)+xf′(x)<0恒成立,若a=2f(2),b=ln2•f(ln2),c=-f(-1),则a,b,c的大小关系为( )
| A、a>b>c |
| B、c>b>a |
| C、a>c>b |
| D、b>c>a |
双曲线2x2-y2=1的离心率为( )
A、
| ||||
B、
| ||||
C、
| ||||
D、
|
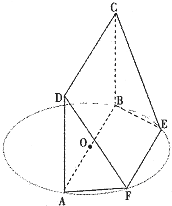 AB为圆O的直径,点E、F在圆上,AB∥EF,矩形ABCD所在平面与圆O所在平面互相垂直,已知AB=2,BC=EF=1.
AB为圆O的直径,点E、F在圆上,AB∥EF,矩形ABCD所在平面与圆O所在平面互相垂直,已知AB=2,BC=EF=1.