题目内容
已知函数f（x）=
，若不等式f（x）＜0的解集为非空集合D，且D⊆（-1，2），则z=2a-b的取值范围为（ ）
|
| A、（4，+∞） |
| B、[-4，+∞） |
| C、（-∞，4） |
| D、（-1，4） |
考点：简单线性规划的应用,分段函数的应用
专题：不等式的解法及应用
分析：根据不等式的解集关系转化为不等式组，利用数形结合以及线性规划的知识进行求解即可得到结论．
解答：
解：∵不等式f（x）＜0的解集为非空集合D，且D⊆（-1，2），
∴等价为
由z=2a-b得b=2a-z，
作出不等式组对应的平面区域如图，
平移直线b=2a-z，由图象可知
当直线b=2a-z经过点A时，直线的截距最大，此时z最小，
由
，解得
，
即A（1，-2），
此时z=2a-b=2-（-2）=4，
故z＞4，
故选：A
∴等价为
|
由z=2a-b得b=2a-z，
作出不等式组对应的平面区域如图，
平移直线b=2a-z，由图象可知
当直线b=2a-z经过点A时，直线的截距最大，此时z最小，
由
|
|
即A（1，-2），
此时z=2a-b=2-（-2）=4，
故z＞4，
故选：A
点评：本题主要考查线性规划的应用，根据不等式的关系转化为不等式组，利用线性规划的知识以及数形结合是解决本题的关键．综合性较强，难度较大．
练习册系列答案
相关题目
定义域为R的奇函数f（x），当x∈（-∞，0）时f（x）+xf′（x）＜0恒成立，若a=2f（2），b=ln2•f（ln2），c=-f（-1），则a，b，c的大小关系为（ ）
| A、a＞b＞c |
| B、c＞b＞a |
| C、a＞c＞b |
| D、b＞c＞a |
双曲线2x2-y2=1的离心率为（ ）
A、
| ||||
B、
| ||||
C、
| ||||
D、
|
已知圆A的方程为（x+1）2+y2=16，点B的坐标为（1，0），P是圆A上任意一点，线段BP的垂直平分线与AP交于点C．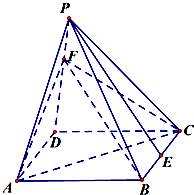
如图，在正四棱锥P-ABCD中，底面是边长为2的正方形，侧棱PA=
如图是某班第1和第2小组学生身高的茎叶图（单位：cm），则这两个小组学生身高中位数的等差中项为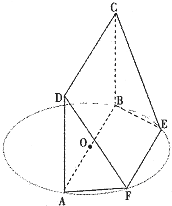
AB为圆O的直径，点E、F在圆上，AB∥EF，矩形ABCD所在平面与圆O所在平面互相垂直，已知AB=2，BC=EF=1．