题目内容
双曲线:
-x2=1的渐近线方程是 .
| y2 |
| 4 |
考点:双曲线的简单性质
专题:圆锥曲线的定义、性质与方程
分析:直接根据双曲线的方程,令方程的右边等于0求出渐近线的方程.
解答:
解:已知双曲线
-x2=1
令:
-x2=0
即得到渐近线方程为:y=±2x
故答案为:y=±2x
| y2 |
| 4 |
令:
| y2 |
| 4 |
即得到渐近线方程为:y=±2x
故答案为:y=±2x
点评:本题考查的知识要点:双曲线的渐渐线方程的求法.

练习册系列答案
相关题目
若直线a平行于平面α,则下列结论错误的是( )
| A、a平行于α内的所有直线 |
| B、α内有无数条直线与a平行 |
| C、直线a上的点到平面α的距离相等 |
| D、α内存在无数条直线与a成90°角 |
若实数x,y满足不等式组
,则z=|x|+2y的最大值是( )
|
| A、10 | B、11 | C、13 | D、14 |
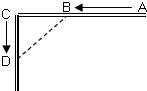 如图,快艇和轮船分别从A地和C地同时开出,航行路线互相垂直,快艇的速度为40千米/时,轮船的速度是15千米/时,A、C两地间的距离是120千米.问经过多少时间.快艇和轮船之间的距离最小?(精确到0.1小时)
如图,快艇和轮船分别从A地和C地同时开出,航行路线互相垂直,快艇的速度为40千米/时,轮船的速度是15千米/时,A、C两地间的距离是120千米.问经过多少时间.快艇和轮船之间的距离最小?(精确到0.1小时)