题目内容
若log2x=log4(x+2),则x= .
考点:对数的运算性质
专题:函数的性质及应用
分析:首先,根据对数的运算性质,化为同底数,然后,根据真数相等,建立等式进行求解.
解答:
解:根据题意,得
log2x=log4(x+2)
=log2
,
∴x=
,
∴x=2.
故答案为:2.
log2x=log4(x+2)
=log2
| x+2 |
∴x=
| x+2 |
∴x=2.
故答案为:2.
点评:本题重点考查了对数的运算性质、方程的求解等知识,属于基础题,灵活掌握对数的运算性质是解题的关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
若函数f(x)=
x3+x2+mx是R上的单调函数,则实数m的取值范围是( )
| 1 |
| 3 |
| A、(1,+∞) |
| B、(-∞,1) |
| C、[1,+∞) |
| D、(-∞,1] |
若直线a平行于平面α,则下列结论错误的是( )
| A、a平行于α内的所有直线 |
| B、α内有无数条直线与a平行 |
| C、直线a上的点到平面α的距离相等 |
| D、α内存在无数条直线与a成90°角 |
若实数x,y满足不等式组
,则z=|x|+2y的最大值是( )
|
| A、10 | B、11 | C、13 | D、14 |
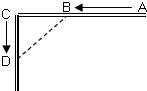 如图,快艇和轮船分别从A地和C地同时开出,航行路线互相垂直,快艇的速度为40千米/时,轮船的速度是15千米/时,A、C两地间的距离是120千米.问经过多少时间.快艇和轮船之间的距离最小?(精确到0.1小时)
如图,快艇和轮船分别从A地和C地同时开出,航行路线互相垂直,快艇的速度为40千米/时,轮船的速度是15千米/时,A、C两地间的距离是120千米.问经过多少时间.快艇和轮船之间的距离最小?(精确到0.1小时)