题目内容
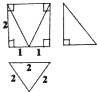
某几何体的三视图如图所示，则该几何体的体积是（ ）
A、
| ||||
B、
| ||||
C、
| ||||
D、
|
考点：由三视图求面积、体积
专题：空间位置关系与距离
分析：由已知的三视图可得：该几何体是一个以主视图为底面的四棱锥，分别求出棱锥的底面面积和高，代入棱锥体积公式，可得答案．
解答：
解：由已知的三视图可得：该几何体是一个以主视图为底面的四棱锥，
其底面面积S=2×2=4，
高h=2×
=
，
故该几何体的体积V=
Sh=
×4×
=
，
故选：D
其底面面积S=2×2=4，
高h=2×
| ||
| 2 |
| 3 |
故该几何体的体积V=
| 1 |
| 3 |
| 1 |
| 3 |
| 3 |
4
| ||
| 3 |
故选：D
点评：根据三视图判断空间几何体的形状，进而求几何的表（侧/底）面积或体积，是高考必考内容，处理的关键是准确判断空间几何体的形状，一般规律是这样的：如果三视图均为三角形，则该几何体必为三棱锥；如果三视图中有两个三角形和一个多边形，则该几何体为N棱锥（N值由另外一个视图的边数确定）；如果三视图中有两个为矩形和一个多边形，则该几何体为N棱柱（N值由另外一个视图的边数确定）；如果三视图中有两个为梯形和一个多边形，则该几何体为N棱柱（N值由另外一个视图的边数确定）；如果三视图中有两个三角形和一个圆，则几何体为圆锥．如果三视图中有两个矩形和一个圆，则几何体为圆柱．如果三视图中有两个梯形和一个圆，则几何体为圆台．
练习册系列答案
相关题目
若实数x，y满足不等式组
，则z=|x|+2y的最大值是（ ）
|
| A、10 | B、11 | C、13 | D、14 |
已知数列{an}的前n项和Sn=
（n=1，2，3，…）
（1）求a1的值；
（2）求证：（n-2）an+1=（n-1）an-1（n≥2）；
（3）判断数列{an}是否为等差数列，并说明理由．
| n(1+an) |
| 2 |
（1）求a1的值；
（2）求证：（n-2）an+1=（n-1）an-1（n≥2）；
（3）判断数列{an}是否为等差数列，并说明理由．
如图，点O为正方体ABCD-A′B′C′D′的中心，点E为面B′BCC′的中心，点F为B′C′的中点，则空间四边形D′OEF在该正方体的各个面上的投影不可能是（ ）
已知函数f（x+1）=x2+2x-5，则f（x）的解析式为（ ）
| A、f（x）=x2 |
| B、f（x）=x2-6 |
| C、f（x）=x2+6 |
| D、f（x）=x2+6x |